Robust Independent Component Analysis by Iterative Maximization of the Kurtosis Contrast with Algebraic Optimal Step Size
Paper and Code
Feb 19, 2010
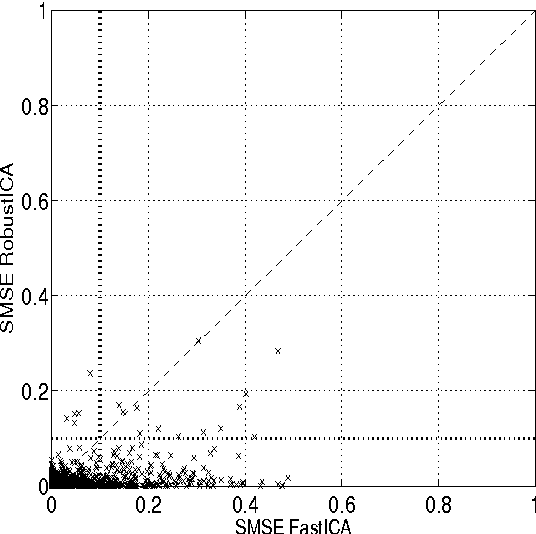


Independent component analysis (ICA) aims at decomposing an observed random vector into statistically independent variables. Deflation-based implementations, such as the popular one-unit FastICA algorithm and its variants, extract the independent components one after another. A novel method for deflationary ICA, referred to as RobustICA, is put forward in this paper. This simple technique consists of performing exact line search optimization of the kurtosis contrast function. The step size leading to the global maximum of the contrast along the search direction is found among the roots of a fourth-degree polynomial. This polynomial rooting can be performed algebraically, and thus at low cost, at each iteration. Among other practical benefits, RobustICA can avoid prewhitening and deals with real- and complex-valued mixtures of possibly noncircular sources alike. The absence of prewhitening improves asymptotic performance. The algorithm is robust to local extrema and shows a very high convergence speed in terms of the computational cost required to reach a given source extraction quality, particularly for short data records. These features are demonstrated by a comparative numerical analysis on synthetic data. RobustICA's capabilities in processing real-world data involving noncircular complex strongly super-Gaussian sources are illustrated by the biomedical problem of atrial activity (AA) extraction in atrial fibrillation (AF) electrocardiograms (ECGs), where it outperforms an alternative ICA-based technique.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge