Initialization Free Graph Based Clustering

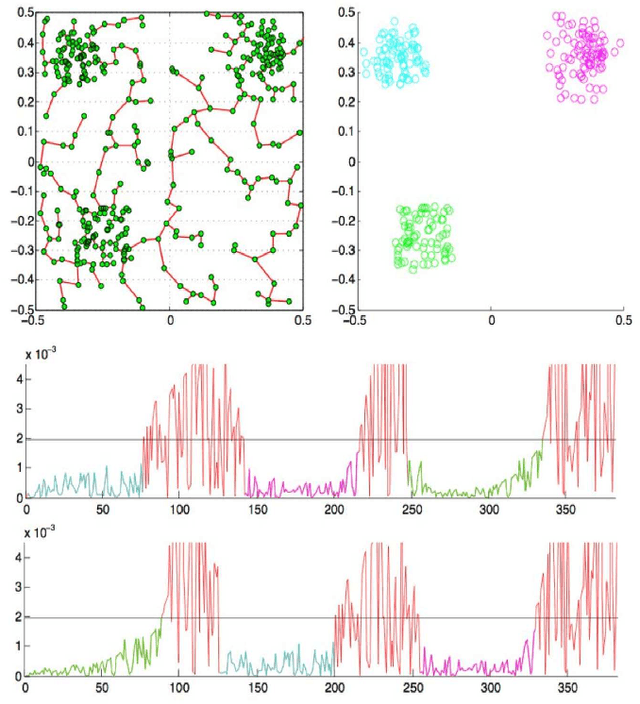
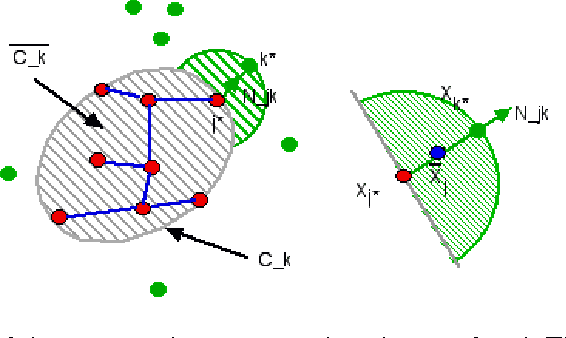
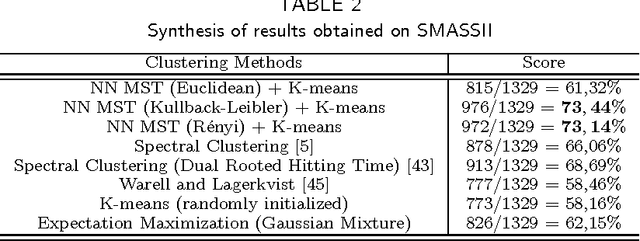
This paper proposes an original approach to cluster multi-component data sets, including an estimation of the number of clusters. From the construction of a minimal spanning tree with Prim's algorithm, and the assumption that the vertices are approximately distributed according to a Poisson distribution, the number of clusters is estimated by thresholding the Prim's trajectory. The corresponding cluster centroids are then computed in order to initialize the generalized Lloyd's algorithm, also known as $K$-means, which allows to circumvent initialization problems. Some results are derived for evaluating the false positive rate of our cluster detection algorithm, with the help of approximations relevant in Euclidean spaces. Metrics used for measuring similarity between multi-dimensional data points are based on symmetrical divergences. The use of these informational divergences together with the proposed method leads to better results, compared to other clustering methods for the problem of astrophysical data processing. Some applications of this method in the multi/hyper-spectral imagery domain to a satellite view of Paris and to an image of the Mars planet are also presented. In order to demonstrate the usefulness of divergences in our problem, the method with informational divergence as similarity measure is compared with the same method using classical metrics. In the astrophysics application, we also compare the method with the spectral clustering algorithms.