Scalable Non-Cartesian Magnetic Resonance Imaging with R2D2
Paper and Code
Mar 27, 2024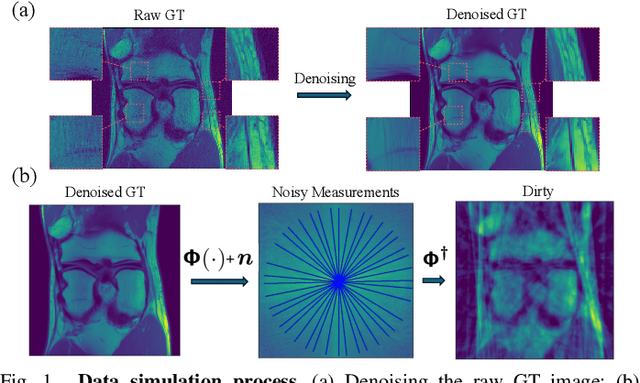
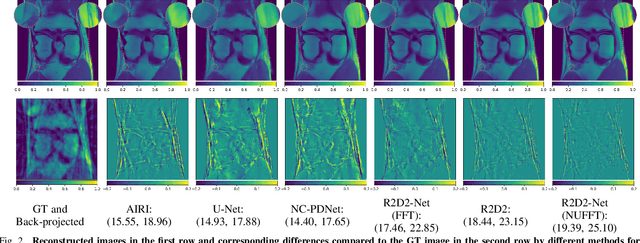
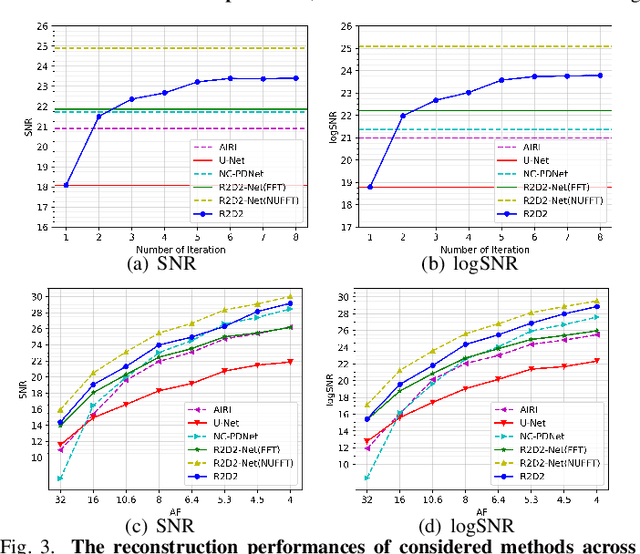
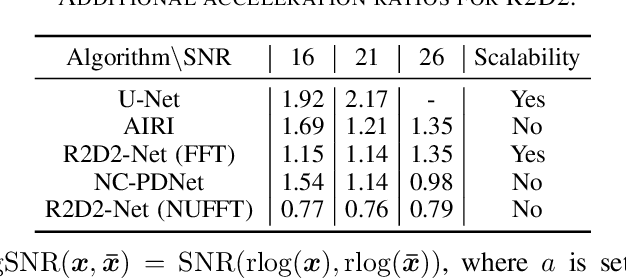
We propose a new approach for non-Cartesian magnetic resonance image reconstruction. While unrolled architectures provide robustness via data-consistency layers, embedding measurement operators in Deep Neural Network (DNN) can become impractical at large scale. Alternative Plug-and-Play (PnP) approaches, where the denoising DNNs are blind to the measurement setting, are not affected by this limitation and have also proven effective, but their highly iterative nature also affects scalability. To address this scalability challenge, we leverage the "Residual-to-Residual DNN series for high-Dynamic range imaging (R2D2)" approach recently introduced in astronomical imaging. R2D2's reconstruction is formed as a series of residual images, iteratively estimated as outputs of DNNs taking the previous iteration's image estimate and associated data residual as inputs. The method can be interpreted as a learned version of the Matching Pursuit algorithm. We demonstrate R2D2 in simulation, considering radial k-space sampling acquisition sequences. Our preliminary results suggest that R2D2 achieves: (i) suboptimal performance compared to its unrolled incarnation R2D2-Net, which is however non-scalable due to the necessary embedding of NUFFT-based data-consistency layers; (ii) superior reconstruction quality to a scalable version of R2D2-Net embedding an FFT-based approximation for data consistency; (iii) superior reconstruction quality to PnP, while only requiring few iterations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge