A deep primal-dual proximal network for image restoration

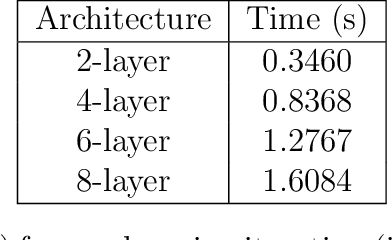
Image restoration remains a challenging task in image processing. Numerous methods have been proposed to tackle this problem, which is often solved by minimizing a non-smooth penalized likelihood function. Although the solution is easily interpretable with theoretic guarantees, its estimation relies on an optimization process. Considering the important research efforts in deep learning for image classification, they offers an alternative to perform image restoration but its adaptation to inverse problem is still challenging. In this work, we design a deep network, named DeepPDNet, built from primal-dual proximal iterations associated with the minimization of a standard penalized likelihood with an analysis prior, allowing us to take advantages from both worlds. We reformulate a specific instance of the Condat-Vu primal-dual hybrid gradient (PDHG) algorithm as a deep network with fixed layers. Each layer corresponds to one iteration of the primal-dual algorithm. The learned parameters are the primal-dual proximal algorithm step-size and the analysis linear operator involved in the penalization. These parameters are allowed to vary from a layer to another one. Two different learning strategies: "Full learning" and "Partial learning" are proposed, the first one is the most efficient numerically while the second one relies on standard constraints insuring convergence in the standard PDHG iterations. Moreover, global and local sparse analysis prior are studied to seek the better feature representation. We experiment the proposed DeepPDNet on the MNIST and BSD68 datasets with different blur and additive Gaussian noise. Extensive results shows that the proposed deep primal-dual proximal networks demonstrate excellent performance on the MNIST dataset compared to other state-of-the-art methods and better or at least comparable performance on the more complex BSD68 dataset.