Sparse hierarchical interaction learning with epigraphical projection
Paper and Code
Dec 18, 2017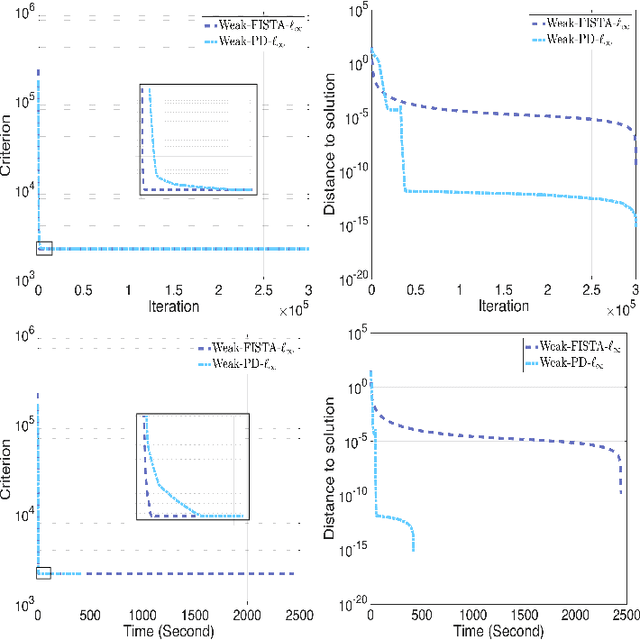
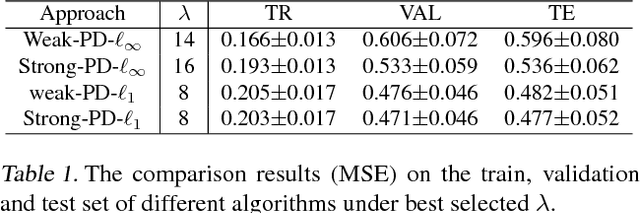
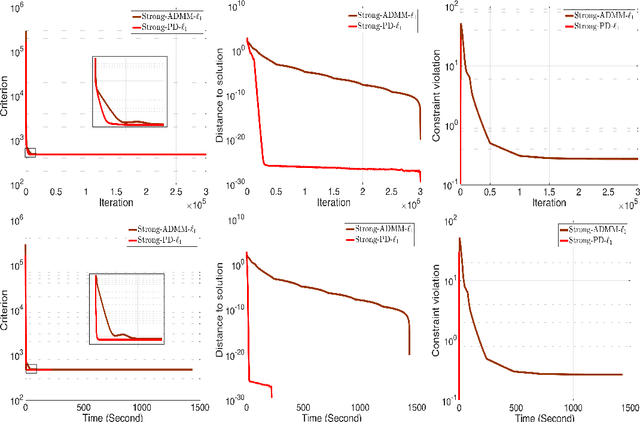
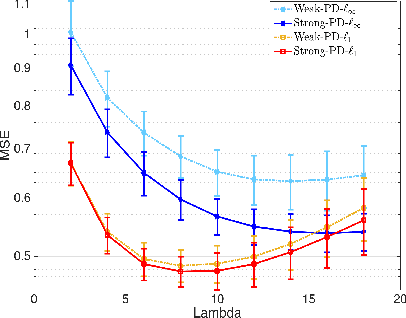
This work focus on regression optimization problem with hierarchical interactions between variables, which is beyond the additive models in the traditional linear regression. We investigate more specifically two different fashions encountered in the literature to deal with this problem: "hierNet" and structural-sparsity regularization, and study their connections. We propose a primal-dual proximal algorithm based on epigraphical projection to optimize a general formulation of this learning problem. The experimental setting first highlights the improvement of the proposed procedure compared to state-of-the-art methods based on fast iterative shrinkage-thresholding algorithm (i.e. FISTA) or alternating direction method of multipliers (i.e. ADMM) and second we provide fair comparisons between the different hierarchical penalizations. The experiments are conducted both on the synthetic and real data, and they clearly show that the proposed primal-dual proximal algorithm based on epigraphical projection is efficient and effective to solve and investigate the question of the hierarchical interaction learning problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge