Dealing with Uncertain Inputs in Regression Trees

Tree-based ensemble methods, as Random Forests and Gradient Boosted Trees, have been successfully used for regression in many applications and research studies. Furthermore, these methods have been extended in order to deal with uncertainty in the output variable, using for example a quantile loss in Random Forests (Meinshausen, 2006). To the best of our knowledge, no extension has been provided yet for dealing with uncertainties in the input variables, even though such uncertainties are common in practical situations. We propose here such an extension by showing how standard regression trees optimizing a quadratic loss can be adapted and learned while taking into account the uncertainties in the input. By doing so, one no longer assumes that an observation lies into a single region of the regression tree, but rather that it belongs to each region with a certain probability. Experiments conducted on several data sets illustrate the good behavior of the proposed extension.

Sparse hierarchical interaction learning with epigraphical projection

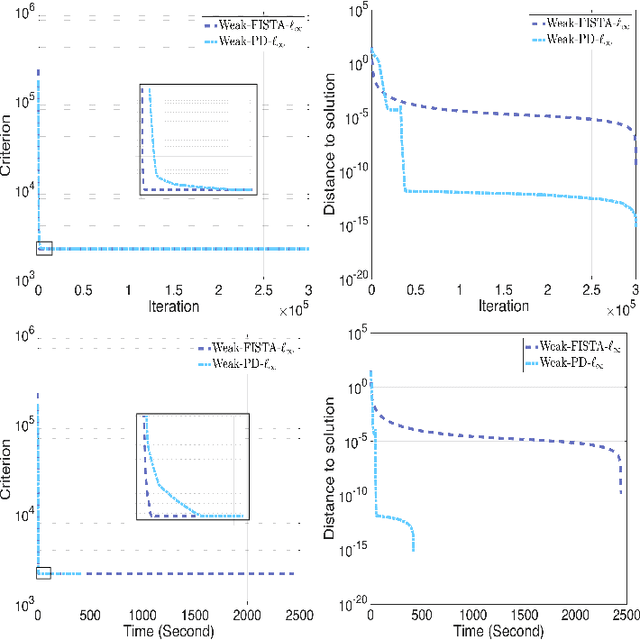
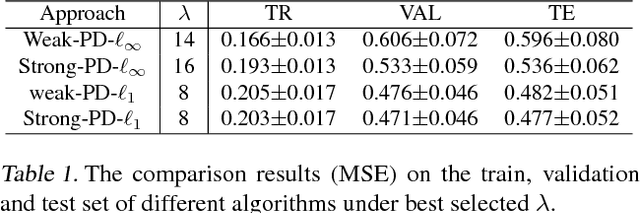
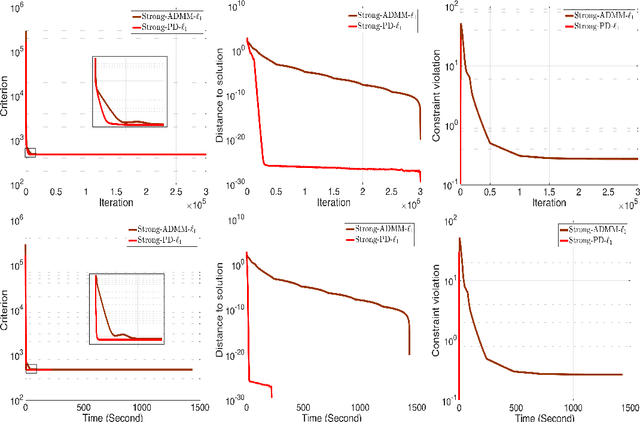
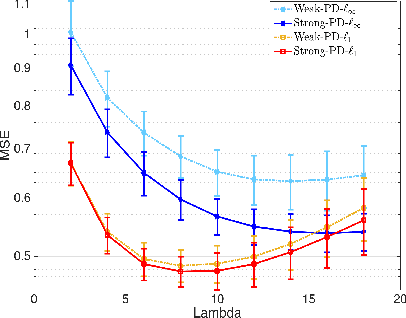
This work focus on regression optimization problem with hierarchical interactions between variables, which is beyond the additive models in the traditional linear regression. We investigate more specifically two different fashions encountered in the literature to deal with this problem: "hierNet" and structural-sparsity regularization, and study their connections. We propose a primal-dual proximal algorithm based on epigraphical projection to optimize a general formulation of this learning problem. The experimental setting first highlights the improvement of the proposed procedure compared to state-of-the-art methods based on fast iterative shrinkage-thresholding algorithm (i.e. FISTA) or alternating direction method of multipliers (i.e. ADMM) and second we provide fair comparisons between the different hierarchical penalizations. The experiments are conducted both on the synthetic and real data, and they clearly show that the proposed primal-dual proximal algorithm based on epigraphical projection is efficient and effective to solve and investigate the question of the hierarchical interaction learning problem.

Semantic Similarity from Natural Language and Ontology Analysis

Artificial Intelligence federates numerous scientific fields in the aim of developing machines able to assist human operators performing complex treatments -- most of which demand high cognitive skills (e.g. learning or decision processes). Central to this quest is to give machines the ability to estimate the likeness or similarity between things in the way human beings estimate the similarity between stimuli. In this context, this book focuses on semantic measures: approaches designed for comparing semantic entities such as units of language, e.g. words, sentences, or concepts and instances defined into knowledge bases. The aim of these measures is to assess the similarity or relatedness of such semantic entities by taking into account their semantics, i.e. their meaning -- intuitively, the words tea and coffee, which both refer to stimulating beverage, will be estimated to be more semantically similar than the words toffee (confection) and coffee, despite that the last pair has a higher syntactic similarity. The two state-of-the-art approaches for estimating and quantifying semantic similarities/relatedness of semantic entities are presented in detail: the first one relies on corpora analysis and is based on Natural Language Processing techniques and semantic models while the second is based on more or less formal, computer-readable and workable forms of knowledge such as semantic networks, thesaurus or ontologies. (...) Beyond a simple inventory and categorization of existing measures, the aim of this monograph is to convey novices as well as researchers of these domains towards a better understanding of semantic similarity estimation and more generally semantic measures.

Semantic Measures for the Comparison of Units of Language, Concepts or Instances from Text and Knowledge Base Analysis

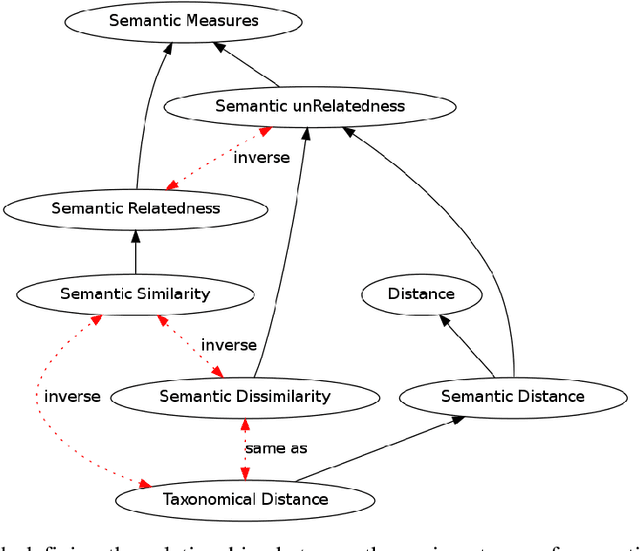
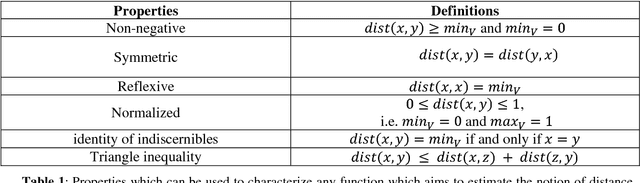
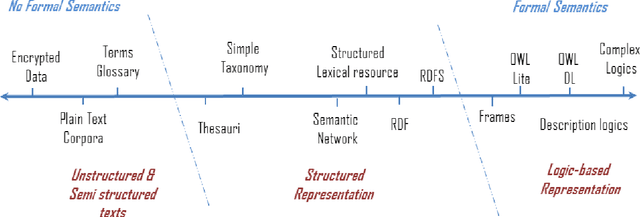
Semantic measures are widely used today to estimate the strength of the semantic relationship between elements of various types: units of language (e.g., words, sentences, documents), concepts or even instances semantically characterized (e.g., diseases, genes, geographical locations). Semantic measures play an important role to compare such elements according to semantic proxies: texts and knowledge representations, which support their meaning or describe their nature. Semantic measures are therefore essential for designing intelligent agents which will for example take advantage of semantic analysis to mimic human ability to compare abstract or concrete objects. This paper proposes a comprehensive survey of the broad notion of semantic measure for the comparison of units of language, concepts or instances based on semantic proxy analyses. Semantic measures generalize the well-known notions of semantic similarity, semantic relatedness and semantic distance, which have been extensively studied by various communities over the last decades (e.g., Cognitive Sciences, Linguistics, and Artificial Intelligence to mention a few).