Exploring the Potential of Bilevel Optimization for Calibrating Neural Networks

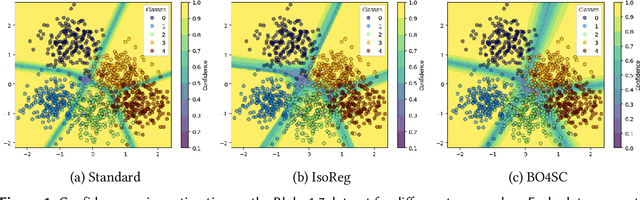
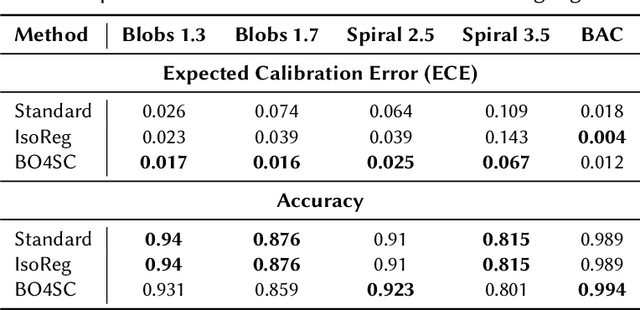
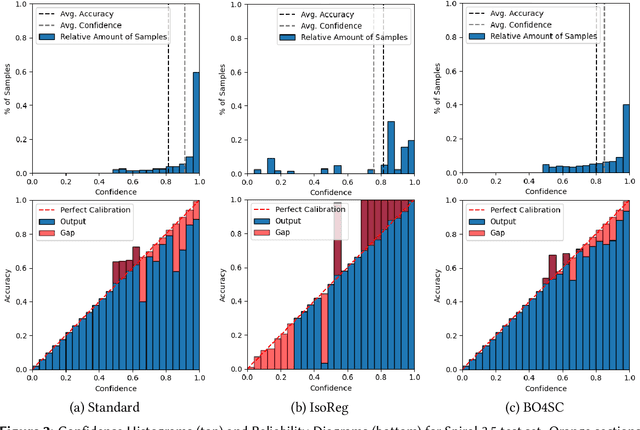
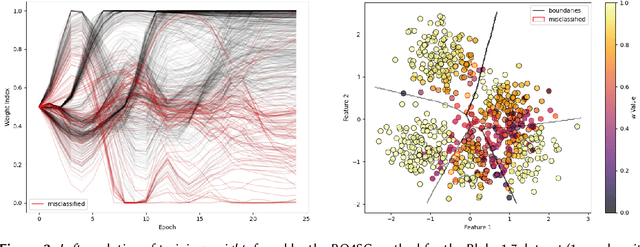
Handling uncertainty is critical for ensuring reliable decision-making in intelligent systems. Modern neural networks are known to be poorly calibrated, resulting in predicted confidence scores that are difficult to use. This article explores improving confidence estimation and calibration through the application of bilevel optimization, a framework designed to solve hierarchical problems with interdependent optimization levels. A self-calibrating bilevel neural-network training approach is introduced to improve a model's predicted confidence scores. The effectiveness of the proposed framework is analyzed using toy datasets, such as Blobs and Spirals, as well as more practical simulated datasets, such as Blood Alcohol Concentration (BAC). It is compared with a well-known and widely used calibration strategy, isotonic regression. The reported experimental results reveal that the proposed bilevel optimization approach reduces the calibration error while preserving accuracy.

Probabilistic Iterative Hard Thresholding for Sparse Learning

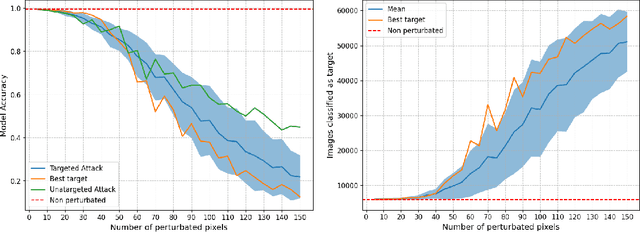
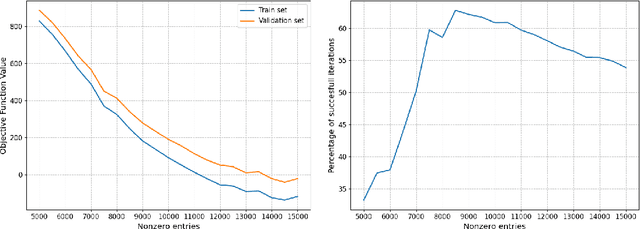
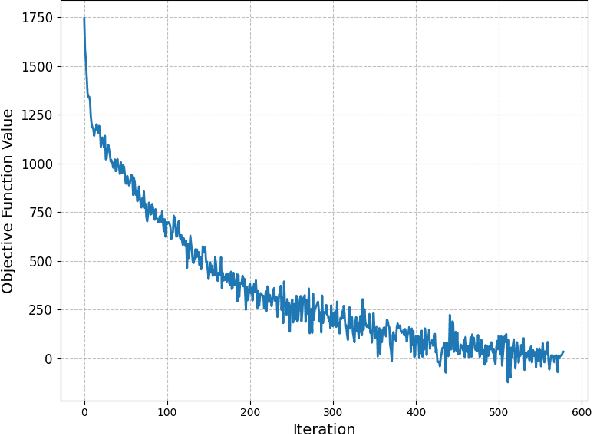
For statistical modeling wherein the data regime is unfavorable in terms of dimensionality relative to the sample size, finding hidden sparsity in the ground truth can be critical in formulating an accurate statistical model. The so-called "l0 norm" which counts the number of non-zero components in a vector, is a strong reliable mechanism of enforcing sparsity when incorporated into an optimization problem. However, in big data settings wherein noisy estimates of the gradient must be evaluated out of computational necessity, the literature is scant on methods that reliably converge. In this paper we present an approach towards solving expectation objective optimization problems with cardinality constraints. We prove convergence of the underlying stochastic process, and demonstrate the performance on two Machine Learning problems.

Relax and penalize: a new bilevel approach to mixed-binary hyperparameter optimization

In recent years, bilevel approaches have become very popular to efficiently estimate high-dimensional hyperparameters of machine learning models. However, to date, binary parameters are handled by continuous relaxation and rounding strategies, which could lead to inconsistent solutions. In this context, we tackle the challenging optimization of mixed-binary hyperparameters by resorting to an equivalent continuous bilevel reformulation based on an appropriate penalty term. We propose an algorithmic framework that, under suitable assumptions, is guaranteed to provide mixed-binary solutions. Moreover, the generality of the method allows to safely use existing continuous bilevel solvers within the proposed framework. We evaluate the performance of our approach for a specific machine learning problem, i.e., the estimation of the group-sparsity structure in regression problems. Reported results clearly show that our method outperforms state-of-the-art approaches based on relaxation and rounding

Learning the Right Layers: a Data-Driven Layer-Aggregation Strategy for Semi-Supervised Learning on Multilayer Graphs

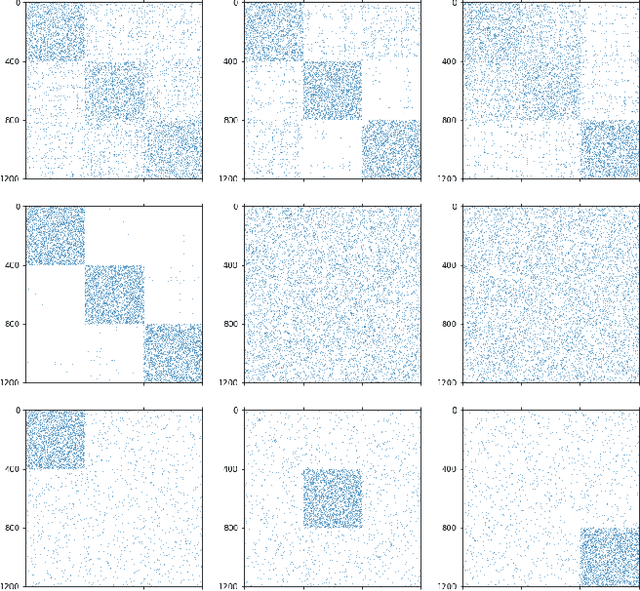
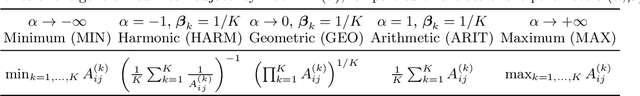
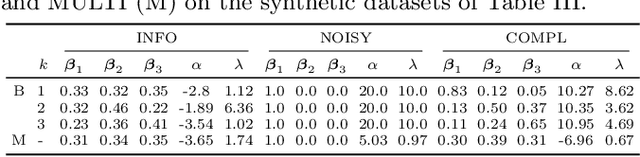
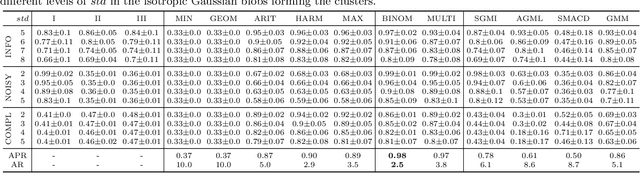
Clustering (or community detection) on multilayer graphs poses several additional complications with respect to standard graphs as different layers may be characterized by different structures and types of information. One of the major challenges is to establish the extent to which each layer contributes to the cluster assignment in order to effectively take advantage of the multilayer structure and improve upon the classification obtained using the individual layers or their union. However, making an informed a-priori assessment about the clustering information content of the layers can be very complicated. In this work, we assume a semi-supervised learning setting, where the class of a small percentage of nodes is initially provided, and we propose a parameter-free Laplacian-regularized model that learns an optimal nonlinear combination of the different layers from the available input labels. The learning algorithm is based on a Frank-Wolfe optimization scheme with inexact gradient, combined with a modified Label Propagation iteration. We provide a detailed convergence analysis of the algorithm and extensive experiments on synthetic and real-world datasets, showing that the proposed method compares favourably with a variety of baselines and outperforms each individual layer when used in isolation.

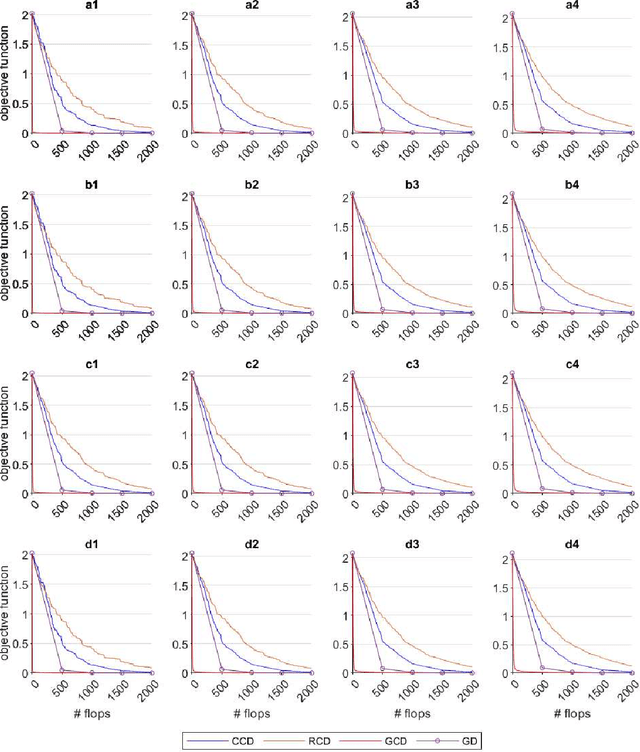
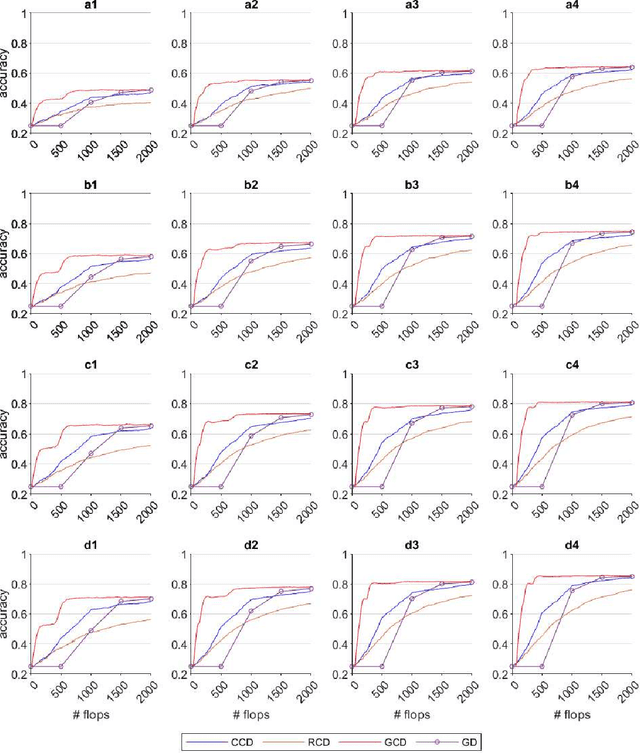
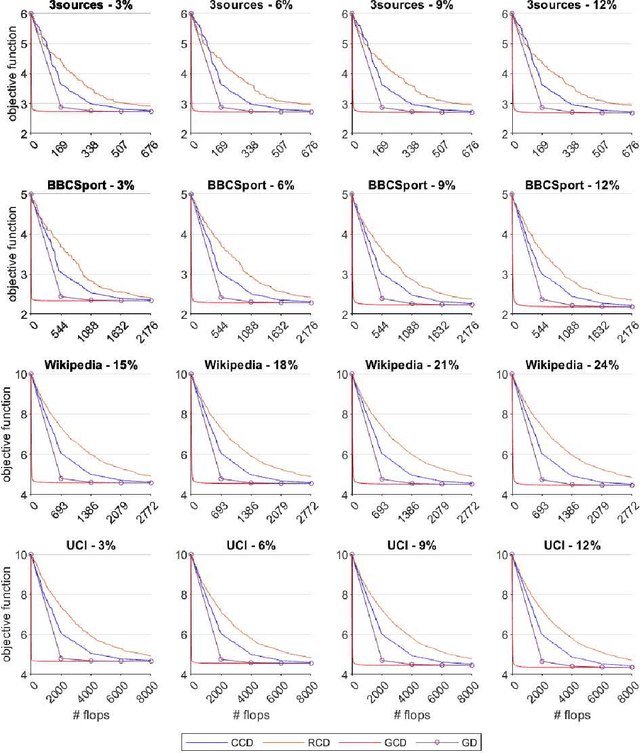
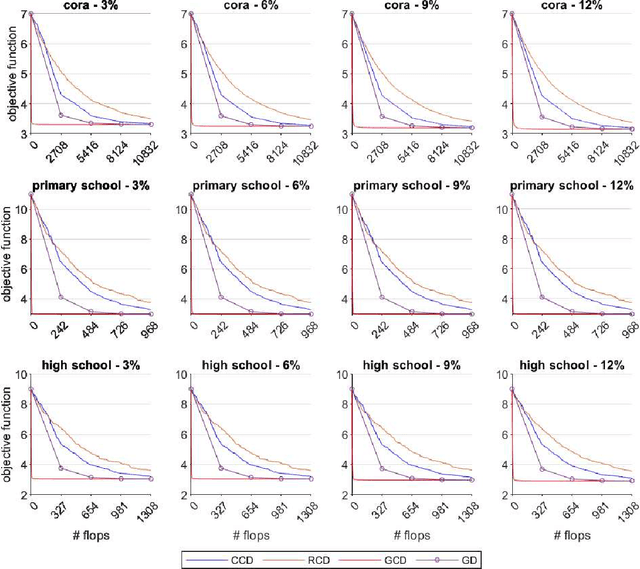
Laplacian-based Semi-Supervised Learning in Multilayer Hypergraphs by Coordinate Descent

Graph Semi-Supervised learning is an important data analysis tool, where given a graph and a set of labeled nodes, the aim is to infer the labels to the remaining unlabeled nodes. In this paper, we start by considering an optimization-based formulation of the problem for an undirected graph, and then we extend this formulation to multilayer hypergraphs. We solve the problem using different coordinate descent approaches and compare the results with the ones obtained by the classic gradient descent method. Experiments on synthetic and real-world datasets show the potential of using coordinate descent methods with suitable selection rules.