Probabilistic Iterative Hard Thresholding for Sparse Learning

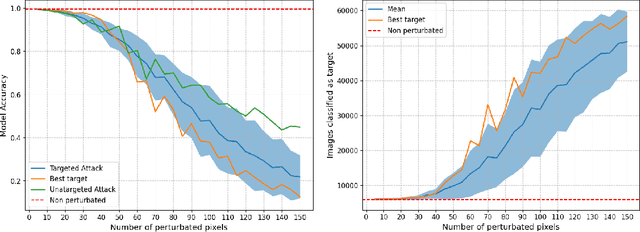
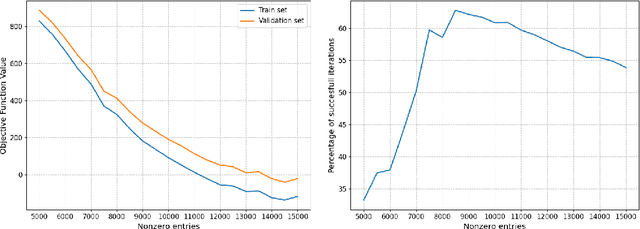
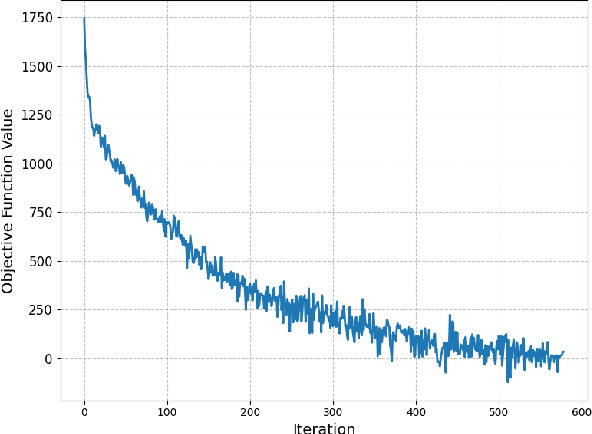
For statistical modeling wherein the data regime is unfavorable in terms of dimensionality relative to the sample size, finding hidden sparsity in the ground truth can be critical in formulating an accurate statistical model. The so-called "l0 norm" which counts the number of non-zero components in a vector, is a strong reliable mechanism of enforcing sparsity when incorporated into an optimization problem. However, in big data settings wherein noisy estimates of the gradient must be evaluated out of computational necessity, the literature is scant on methods that reliably converge. In this paper we present an approach towards solving expectation objective optimization problems with cardinality constraints. We prove convergence of the underlying stochastic process, and demonstrate the performance on two Machine Learning problems.

Improving Performance in Neural Networks by Dendrites-Activated Connections

Computational units in artificial neural networks follow a simplified model of biological neurons. In the biological model, the output signal of a neuron runs down the axon, splits following the many branches at its end, and passes identically to all the downward neurons of the network. Each of the downward neurons will use their copy of this signal as one of many inputs dendrites, integrate them all and fire an output, if above some threshold. In the artificial neural network, this translates to the fact that the nonlinear filtering of the signal is performed in the upward neuron, meaning that in practice the same activation is shared between all the downward neurons that use that signal as their input. Dendrites thus play a passive role. We propose a slightly more complex model for the biological neuron, where dendrites play an active role: the activation in the output of the upward neuron becomes optional, and instead the signals going through each dendrite undergo independent nonlinear filterings, before the linear combination. We implement this new model into a ReLU computational unit and discuss its biological plausibility. We compare this new computational unit with the standard one and describe it from a geometrical point of view. We provide a Keras implementation of this unit into fully connected and convolutional layers and estimate their FLOPs and weights change. We then use these layers in ResNet architectures on CIFAR-10, CIFAR-100, Imagenette, and Imagewoof, obtaining performance improvements over standard ResNets up to 1.73%. Finally, we prove a universal representation theorem for continuous functions on compact sets and show that this new unit has more representational power than its standard counterpart.