Achieving Predictive Precision: Leveraging LSTM and Pseudo Labeling for Volvo's Discovery Challenge at ECML-PKDD 2024

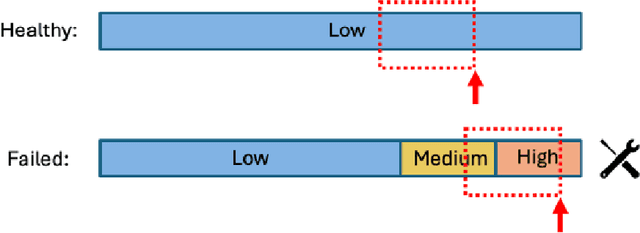
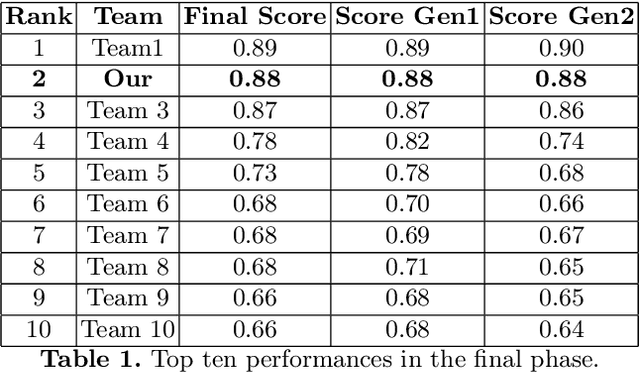
This paper presents the second-place methodology in the Volvo Discovery Challenge at ECML-PKDD 2024, where we used Long Short-Term Memory networks and pseudo-labeling to predict maintenance needs for a component of Volvo trucks. We processed the training data to mirror the test set structure and applied a base LSTM model to label the test data iteratively. This approach refined our model's predictive capabilities and culminated in a macro-average F1-score of 0.879, demonstrating robust performance in predictive maintenance. This work provides valuable insights for applying machine learning techniques effectively in industrial settings.

A Systematization of the Wagner Framework: Graph Theory Conjectures and Reinforcement Learning

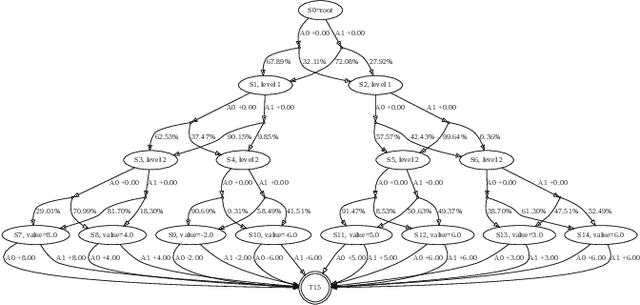
In 2021, Adam Zsolt Wagner proposed an approach to disprove conjectures in graph theory using Reinforcement Learning (RL). Wagner's idea can be framed as follows: consider a conjecture, such as a certain quantity f(G) < 0 for every graph G; one can then play a single-player graph-building game, where at each turn the player decides whether to add an edge or not. The game ends when all edges have been considered, resulting in a certain graph G_T, and f(G_T) is the final score of the game; RL is then used to maximize this score. This brilliant idea is as simple as innovative, and it lends itself to systematic generalization. Several different single-player graph-building games can be employed, along with various RL algorithms. Moreover, RL maximizes the cumulative reward, allowing for step-by-step rewards instead of a single final score, provided the final cumulative reward represents the quantity of interest f(G_T). In this paper, we discuss these and various other choices that can be significant in Wagner's framework. As a contribution to this systematization, we present four distinct single-player graph-building games. Each game employs both a step-by-step reward system and a single final score. We also propose a principled approach to select the most suitable neural network architecture for any given conjecture, and introduce a new dataset of graphs labeled with their Laplacian spectra. Furthermore, we provide a counterexample for a conjecture regarding the sum of the matching number and the spectral radius, which is simpler than the example provided in Wagner's original paper. The games have been implemented as environments in the Gymnasium framework, and along with the dataset, are available as open-source supplementary materials.

GloNets: Globally Connected Neural Networks

Deep learning architectures suffer from depth-related performance degradation, limiting the effective depth of neural networks. Approaches like ResNet are able to mitigate this, but they do not completely eliminate the problem. We introduce Globally Connected Neural Networks (GloNet), a novel architecture overcoming depth-related issues, designed to be superimposed on any model, enhancing its depth without increasing complexity or reducing performance. With GloNet, the network's head uniformly receives information from all parts of the network, regardless of their level of abstraction. This enables GloNet to self-regulate information flow during training, reducing the influence of less effective deeper layers, and allowing for stable training irrespective of network depth. This paper details GloNet's design, its theoretical basis, and a comparison with existing similar architectures. Experiments show GloNet's self-regulation ability and resilience to depth-related learning challenges, like performance degradation. Our findings suggest GloNet as a strong alternative to traditional architectures like ResNets.

Improving Performance in Neural Networks by Dendrites-Activated Connections

Computational units in artificial neural networks follow a simplified model of biological neurons. In the biological model, the output signal of a neuron runs down the axon, splits following the many branches at its end, and passes identically to all the downward neurons of the network. Each of the downward neurons will use their copy of this signal as one of many inputs dendrites, integrate them all and fire an output, if above some threshold. In the artificial neural network, this translates to the fact that the nonlinear filtering of the signal is performed in the upward neuron, meaning that in practice the same activation is shared between all the downward neurons that use that signal as their input. Dendrites thus play a passive role. We propose a slightly more complex model for the biological neuron, where dendrites play an active role: the activation in the output of the upward neuron becomes optional, and instead the signals going through each dendrite undergo independent nonlinear filterings, before the linear combination. We implement this new model into a ReLU computational unit and discuss its biological plausibility. We compare this new computational unit with the standard one and describe it from a geometrical point of view. We provide a Keras implementation of this unit into fully connected and convolutional layers and estimate their FLOPs and weights change. We then use these layers in ResNet architectures on CIFAR-10, CIFAR-100, Imagenette, and Imagewoof, obtaining performance improvements over standard ResNets up to 1.73%. Finally, we prove a universal representation theorem for continuous functions on compact sets and show that this new unit has more representational power than its standard counterpart.

Leela Zero Score: a Study of a Score-based AlphaGo Zero

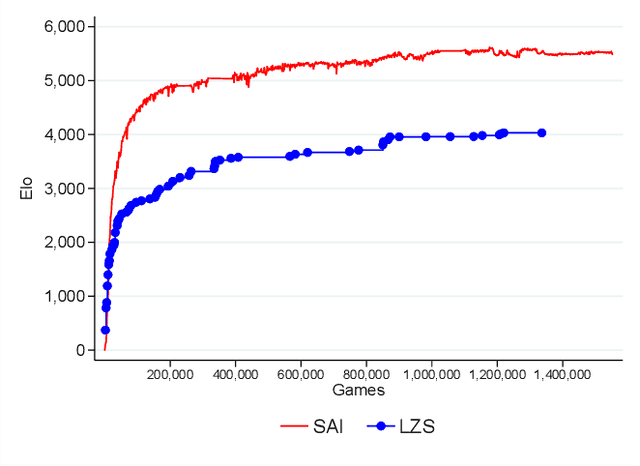
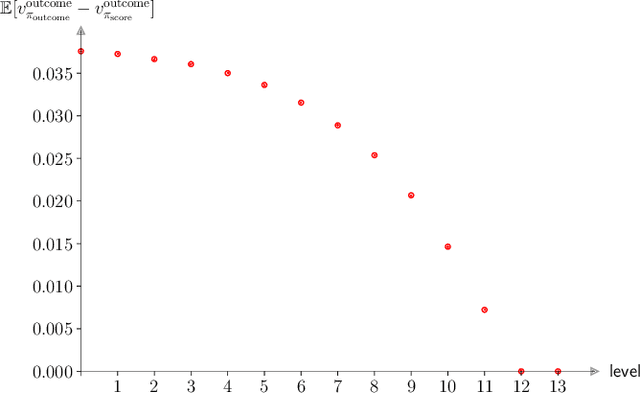
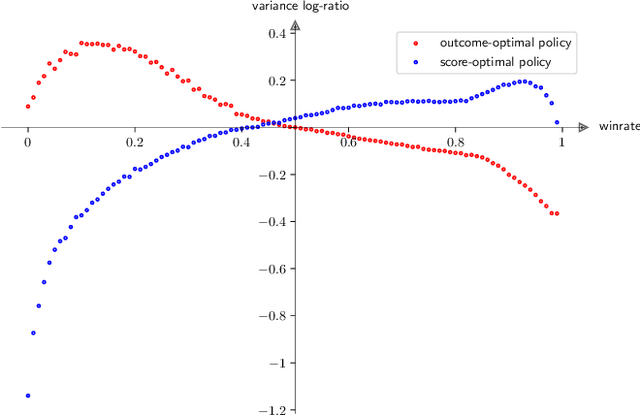
AlphaGo, AlphaGo Zero, and all of their derivatives can play with superhuman strength because they are able to predict the win-lose outcome with great accuracy. However, Go as a game is decided by a final score difference, and in final positions AlphaGo plays suboptimal moves: this is not surprising, since AlphaGo is completely unaware of the final score difference, all winning final positions being equivalent from the winrate perspective. This can be an issue, for instance when trying to learn the "best" move or to play with an initial handicap. Moreover, there is the theoretical quest of the "perfect game", that is, the minimax solution. Thus, a natural question arises: is it possible to train a successful Reinforcement Learning agent to predict score differences instead of winrates? No empirical or theoretical evidence can be found in the literature to support the folklore statement that "this does not work". In this paper we present Leela Zero Score, a software designed to support or disprove the "does not work" statement. Leela Zero Score is designed on the open-source solution known as Leela Zero, and is trained on a 9x9 board to predict score differences instead of winrates. We find that the training produces a rational player, and we analyze its style against a strong amateur human player, to find that it is prone to some mistakes when the outcome is close. We compare its strength against SAI, an AlphaGo Zero-like software working on the 9x9 board, and find that the training of Leela Zero Score has reached a premature convergence to a player weaker than SAI.

SAI: a Sensible Artificial Intelligence that plays with handicap and targets high scores in 9x9 Go (extended version)

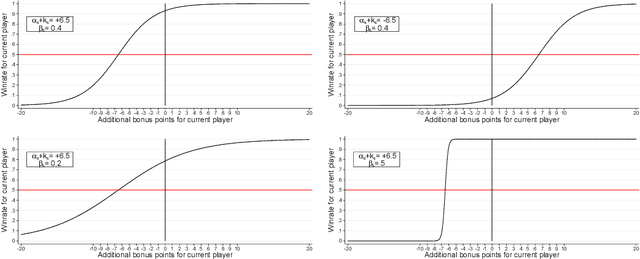
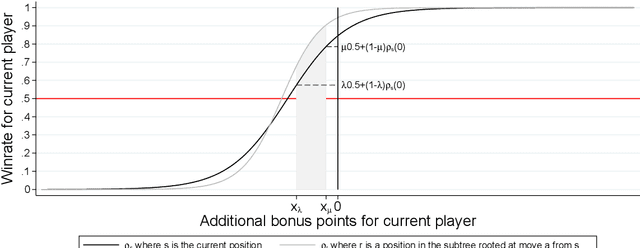
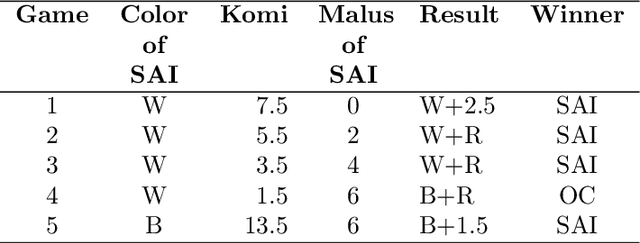
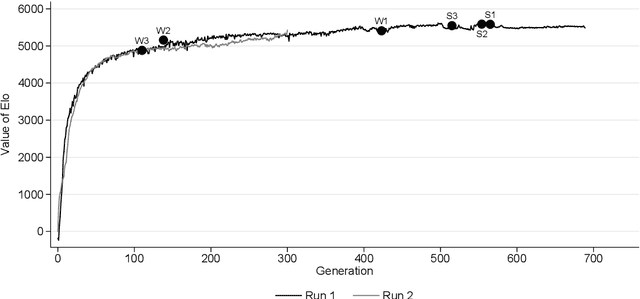
We develop a new model that can be applied to any perfect information two-player zero-sum game to target a high score, and thus a perfect play. We integrate this model into the Monte Carlo tree search-policy iteration learning pipeline introduced by Google DeepMind with AlphaGo. Training this model on 9x9 Go produces a superhuman Go player, thus proving that it is stable and robust. We show that this model can be used to effectively play with both positional and score handicap. We develop a family of agents that can target high scores against any opponent, and recover from very severe disadvantage against weak opponents. To the best of our knowledge, these are the first effective achievements in this direction.

SAI, a Sensible Artificial Intelligence that plays Go

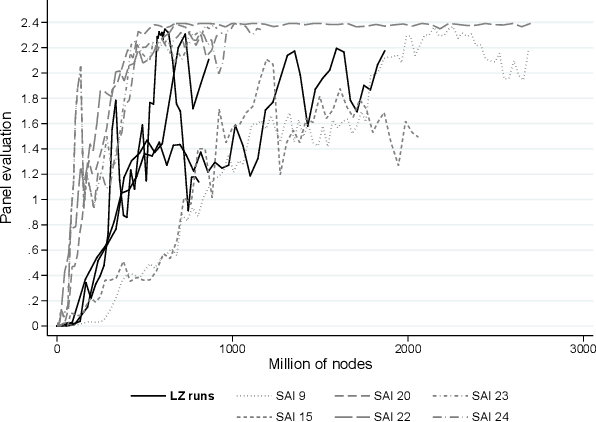
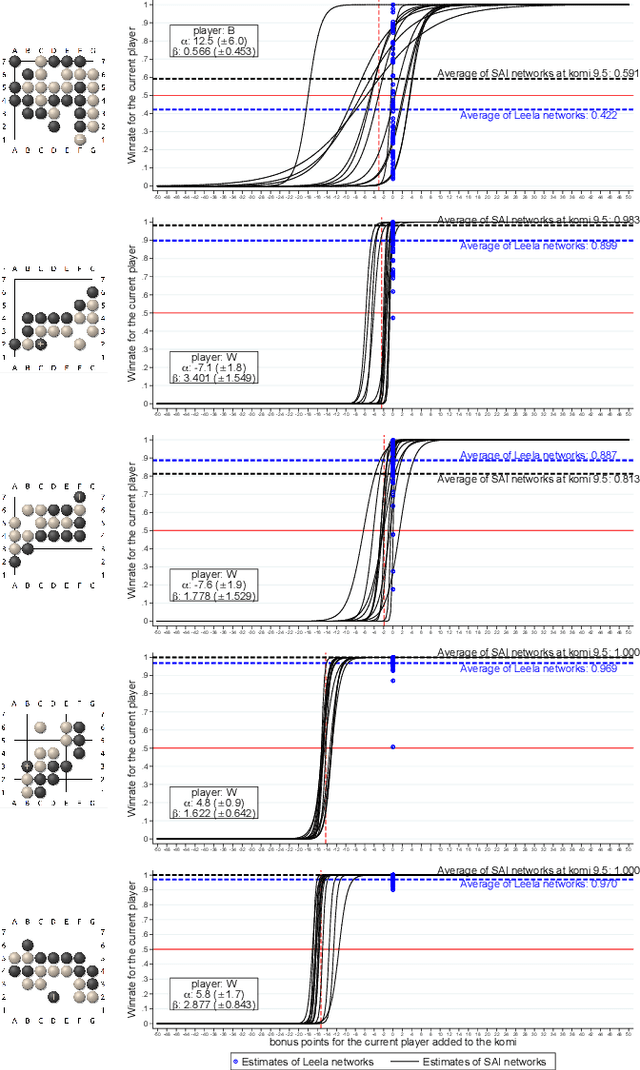
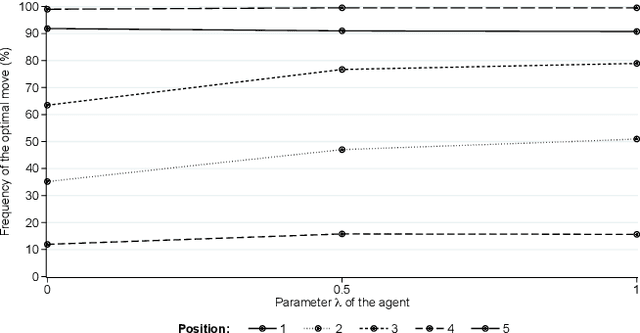
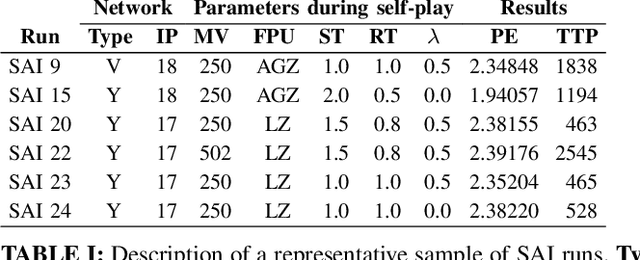
We propose a multiple-komi modification of the AlphaGo Zero/Leela Zero paradigm. The winrate as a function of the komi is modeled with a two-parameters sigmoid function, so that the neural network must predict just one more variable to assess the winrate for all komi values. A second novel feature is that training is based on self-play games that occasionaly branch -with changed komi- when the position is uneven. With this setting, reinforcement learning is showed to work on 7x7 Go, obtaining very strong playing agents. As a useful byproduct, the sigmoid parameters given by the network allow to estimate the score difference on the board, and to evaluate how much the game is decided.