Increasing the clock speed of a thermodynamic computer by adding noise

We describe a proposal for increasing the effective clock speed of a thermodynamic computer, by altering the interaction scale of the units within the computer and introducing to the computer an additional source of noise. The resulting thermodynamic computer program is equivalent to the original computer program, but runs at a higher clock speed. This approach offers a way of increasing the speed of thermodynamic computing while preserving the fidelity of computation.

Adaptive AI-Driven Material Synthesis: Towards Autonomous 2D Materials Growth

Two-dimensional (2D) materials are poised to revolutionize current solid-state technology with their extraordinary properties. Yet, the primary challenge remains their scalable production. While there have been significant advancements, much of the scientific progress has depended on the exfoliation of materials, a method that poses severe challenges for large-scale applications. With the advent of artificial intelligence (AI) in materials science, innovative synthesis methodologies are now on the horizon. This study explores the forefront of autonomous materials synthesis using an artificial neural network (ANN) trained by evolutionary methods, focusing on the efficient production of graphene. Our approach demonstrates that a neural network can iteratively and autonomously learn a time-dependent protocol for the efficient growth of graphene, without requiring pretraining on what constitutes an effective recipe. Evaluation criteria are based on the proximity of the Raman signature to that of monolayer graphene: higher scores are granted to outcomes whose spectrum more closely resembles that of an ideal continuous monolayer structure. This feedback mechanism allows for iterative refinement of the ANN's time-dependent synthesis protocols, progressively improving sample quality. Through the advancement and application of AI methodologies, this work makes a substantial contribution to the field of materials engineering, fostering a new era of innovation and efficiency in the synthesis process.

Oscillatrons: neural units with time-dependent multifunctionality

Several branches of computing use a system's physical dynamics to do computation. We show that the dynamics of an underdamped harmonic oscillator can perform multifunctional computation, solving distinct problems at distinct times within a dynamical trajectory. Oscillator computing usually focuses on the oscillator's phase as the information-carrying component. Here we focus on the time-resolved amplitude of an oscillator whose inputs influence its frequency, which has a natural parallel as the activity of a time-dependent neural unit. We call this unit an oscillatron. The activity of an oscillatron at fixed time is a nonmonotonic function of the input, and so it can solve nonlinearly-separable problems such as XOR. The activity of the oscillatron at fixed input is a nonmonotonic function of time, and so it is multifunctional in a temporal sense, able to carry out distinct nonlinear computations at distinct times within the same dynamical trajectory. Time-resolved computing of this nature can be done in or out of equilibrium, with the natural time evolution of the system giving us multiple computations for the price of one.

Springs and a stopwatch: neural units with time-dependent multifunctionality

Several branches of computing use a system's physical dynamics to do computation. We show that the dynamics of an underdamped harmonic oscillator can perform multifunctional computation, solving distinct problems at distinct times within a single dynamical trajectory. Oscillator computing usually focuses on the oscillator's phase as the information-carrying component. Here we focus on the time-resolved amplitude of an oscillator whose inputs influence its frequency, which has a natural parallel as the activity of a time-dependent neural unit. Because the activity of the unit at fixed time is a nonmonotonic function of the input, the unit can solve nonlinearly-separable problems such as XOR. Because the activity of the unit at fixed input is a nonmonotonic function of time, the unit is multifunctional in a temporal sense, able to carry out distinct nonlinear computations at distinct times within the same dynamical trajectory. Time-resolved computing of this nature can be done in or out of equilibrium, with the natural time evolution of the system giving us multiple computations for the price of one.

How to train your demon to do fast information erasure without heat production

Time-dependent protocols that perform irreversible logical operations, such as memory erasure, cost work and produce heat, placing bounds on the efficiency of computers. Here we use a prototypical computer model of a physical memory to show that it is possible to learn feedback-control protocols to do fast memory erasure without input of work or production of heat. These protocols, which are enacted by a neural-network "demon", do not violate the second law of thermodynamics because the demon generates more heat than the memory absorbs. The result is a form of nonlocal heat exchange in which one computation is rendered energetically favorable while a compensating one produces heat elsewhere, a tactic that could be used to rationally design the flow of energy within a computer.

Demon in the machine: learning to extract work and absorb entropy from fluctuating nanosystems

We use Monte Carlo and genetic algorithms to train neural-network feedback-control protocols for simulated fluctuating nanosystems. These protocols convert the information obtained by the feedback process into heat or work, allowing the extraction of work from a colloidal particle pulled by an optical trap and the absorption of entropy by an Ising model undergoing magnetization reversal. The learning framework requires no prior knowledge of the system, depends only upon measurements that are accessible experimentally, and scales to systems of considerable complexity. It could be used in the laboratory to learn protocols for fluctuating nanosystems that convert measurement information into stored work or heat.

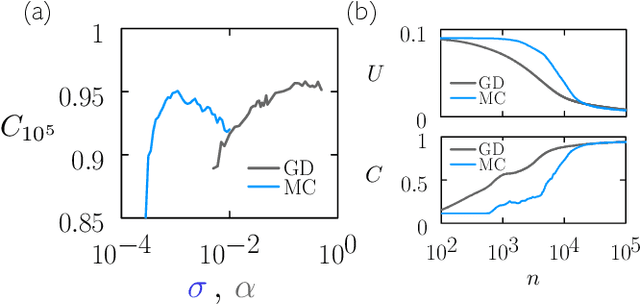
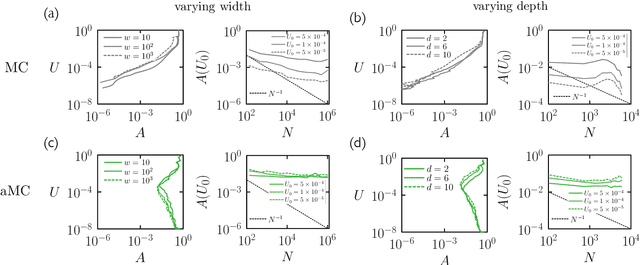
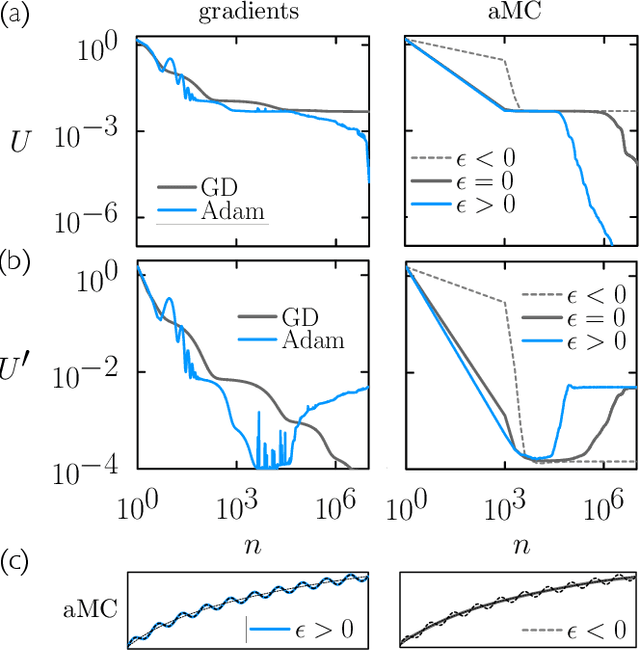
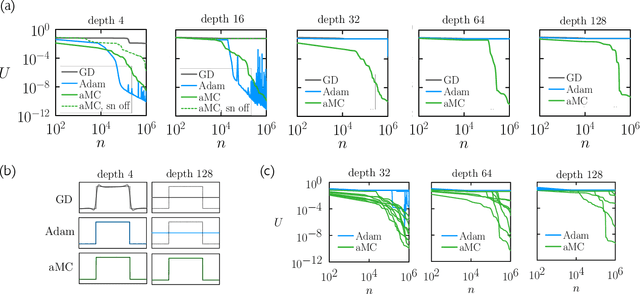
Training neural networks using Metropolis Monte Carlo and an adaptive variant

We examine the zero-temperature Metropolis Monte Carlo algorithm as a tool for training a neural network by minimizing a loss function. We find that, as expected on theoretical grounds and shown empirically by other authors, Metropolis Monte Carlo can train a neural net with an accuracy comparable to that of gradient descent, if not necessarily as quickly. The Metropolis algorithm does not fail automatically when the number of parameters of a neural network is large. It can fail when a neural network's structure or neuron activations are strongly heterogenous, and we introduce an adaptive Monte Carlo algorithm, aMC, to overcome these limitations. The intrinsic stochasticity of the Monte Carlo method allows aMC to train neural networks in which the gradient is too small to allow training by gradient descent. We suggest that, as for molecular simulation, Monte Carlo methods offer a complement to gradient-based methods for training neural networks, allowing access to a distinct set of network architectures and principles.

Cellular automata can classify data by inducing trajectory phase coexistence

We show that cellular automata can classify data by inducing a form of dynamical phase coexistence. We use Monte Carlo methods to search for general two-dimensional deterministic automata that classify images on the basis of activity, the number of state changes that occur in a trajectory initiated from the image. When the depth of the automaton is a trainable parameter, the search scheme identifies automata that generate a population of dynamical trajectories displaying high or low activity, depending on initial conditions. Automata of this nature behave as nonlinear activation functions with an output that is effectively binary, resembling an emergent version of a spiking neuron. Our work connects machine learning and reservoir computing to phenomena conceptually similar to those seen in physical systems such as magnets and glasses.

Learning stochastic dynamics and predicting emergent behavior using transformers

We show that a neural network originally designed for language processing can learn the dynamical rules of a stochastic system by observation of a single dynamical trajectory of the system, and can accurately predict its emergent behavior under conditions not observed during training. We consider a lattice model of active matter undergoing continuous-time Monte Carlo dynamics, simulated at a density at which its steady state comprises small, dispersed clusters. We train a neural network called a transformer on a single trajectory of the model. The transformer, which we show has the capacity to represent dynamical rules that are numerous and nonlocal, learns that the dynamics of this model consists of a small number of processes. Forward-propagated trajectories of the trained transformer, at densities not encountered during training, exhibit motility-induced phase separation and so predict the existence of a nonequilibrium phase transition. Transformers have the flexibility to learn dynamical rules from observation without explicit enumeration of rates or coarse-graining of configuration space, and so the procedure used here can be applied to a wide range of physical systems, including those with large and complex dynamical generators.

Neuroevolutionary learning of particles and protocols for self-assembly

Within simulations of molecules deposited on a surface we show that neuroevolutionary learning can design particles and time-dependent protocols to promote self-assembly, without input from physical concepts such as thermal equilibrium or mechanical stability and without prior knowledge of candidate or competing structures. The learning algorithm is capable of both directed and exploratory design: it can assemble a material with a user-defined property, or search for novelty in the space of specified order parameters. In the latter mode it explores the space of what can be made rather than the space of structures that are low in energy but not necessarily kinetically accessible.