Missing Wedge Inpainting and Joint Alignment in Electron Tomography through Implicit Neural Representations

Electron tomography is a powerful tool for understanding the morphology of materials in three dimensions, but conventional reconstruction algorithms typically suffer from missing-wedge artifacts and data misalignment imposed by experimental constraints. Recently proposed supervised machine-learning-enabled reconstruction methods to address these challenges rely on training data and are therefore difficult to generalize across materials systems. We propose a fully self-supervised implicit neural representation (INR) approach using a neural network as a regularizer. Our approach enables fast inline alignment through pose optimization, missing wedge inpainting, and denoising of low dose datasets via model regularization using only a single dataset. We apply our method to simulated and experimental data and show that it produces high-quality tomograms from diverse and information limited datasets. Our results show that INR-based self-supervised reconstructions offer high fidelity reconstructions with minimal user input and preprocessing, and can be readily applied to a wide variety of materials samples and experimental parameters.

Thermodynamic computing out of equilibrium

We present the design for a thermodynamic computer that can perform arbitrary nonlinear calculations in or out of equilibrium. Simple thermodynamic circuits, fluctuating degrees of freedom in contact with a thermal bath and confined by a quartic potential, display an activity that is a nonlinear function of their input. Such circuits can therefore be regarded as thermodynamic neurons, and can serve as the building blocks of networked structures that act as thermodynamic neural networks, universal function approximators whose operation is powered by thermal fluctuations. We simulate a digital model of a thermodynamic neural network, and show that its parameters can be adjusted by genetic algorithm to perform nonlinear calculations at specified observation times, regardless of whether the system has attained thermal equilibrium. This work expands the field of thermodynamic computing beyond the regime of thermal equilibrium, enabling fully nonlinear computations, analogous to those performed by classical neural networks, at specified observation times.

Adaptive AI-Driven Material Synthesis: Towards Autonomous 2D Materials Growth

Two-dimensional (2D) materials are poised to revolutionize current solid-state technology with their extraordinary properties. Yet, the primary challenge remains their scalable production. While there have been significant advancements, much of the scientific progress has depended on the exfoliation of materials, a method that poses severe challenges for large-scale applications. With the advent of artificial intelligence (AI) in materials science, innovative synthesis methodologies are now on the horizon. This study explores the forefront of autonomous materials synthesis using an artificial neural network (ANN) trained by evolutionary methods, focusing on the efficient production of graphene. Our approach demonstrates that a neural network can iteratively and autonomously learn a time-dependent protocol for the efficient growth of graphene, without requiring pretraining on what constitutes an effective recipe. Evaluation criteria are based on the proximity of the Raman signature to that of monolayer graphene: higher scores are granted to outcomes whose spectrum more closely resembles that of an ideal continuous monolayer structure. This feedback mechanism allows for iterative refinement of the ANN's time-dependent synthesis protocols, progressively improving sample quality. Through the advancement and application of AI methodologies, this work makes a substantial contribution to the field of materials engineering, fostering a new era of innovation and efficiency in the synthesis process.

Learning stochastic dynamics and predicting emergent behavior using transformers

We show that a neural network originally designed for language processing can learn the dynamical rules of a stochastic system by observation of a single dynamical trajectory of the system, and can accurately predict its emergent behavior under conditions not observed during training. We consider a lattice model of active matter undergoing continuous-time Monte Carlo dynamics, simulated at a density at which its steady state comprises small, dispersed clusters. We train a neural network called a transformer on a single trajectory of the model. The transformer, which we show has the capacity to represent dynamical rules that are numerous and nonlocal, learns that the dynamics of this model consists of a small number of processes. Forward-propagated trajectories of the trained transformer, at densities not encountered during training, exhibit motility-induced phase separation and so predict the existence of a nonequilibrium phase transition. Transformers have the flexibility to learn dynamical rules from observation without explicit enumeration of rates or coarse-graining of configuration space, and so the procedure used here can be applied to a wide range of physical systems, including those with large and complex dynamical generators.

Dynamical large deviations of two-dimensional kinetically constrained models using a neural-network state ansatz

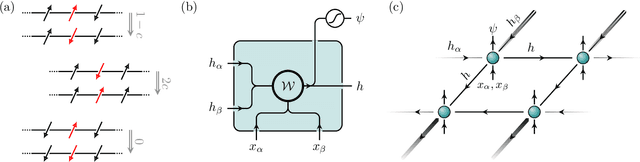
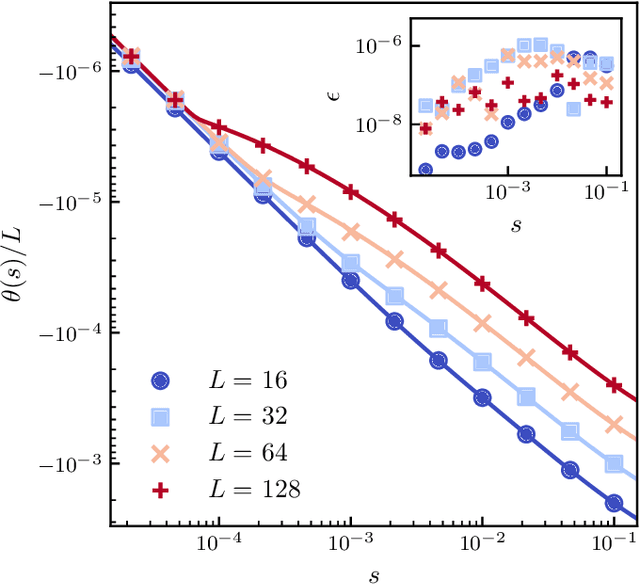
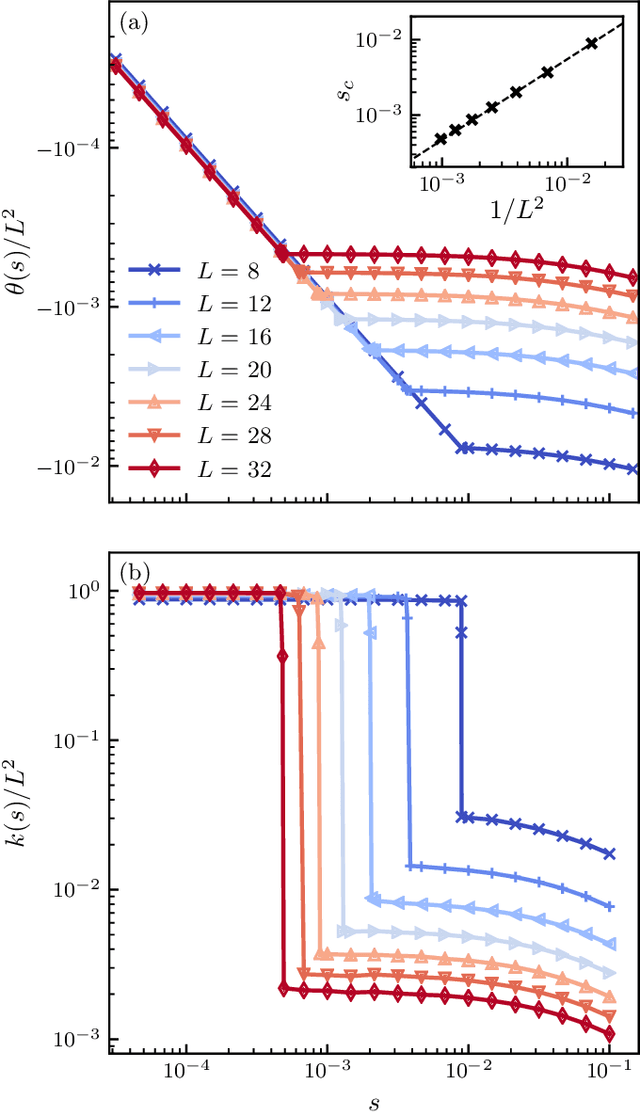
We use a neural network ansatz originally designed for the variational optimization of quantum systems to study dynamical large deviations in classical ones. We obtain the scaled cumulant-generating function for the dynamical activity of the Fredrickson-Andersen model, a prototypical kinetically constrained model, in one and two dimensions, and present the first size-scaling analysis of the dynamical activity in two dimensions. These results provide a new route to the study of dynamical large-deviation functions, and highlight the broad applicability of the neural-network state ansatz across domains in physics.