DLGNet: Hyperedge Classification through Directed Line Graphs for Chemical Reactions

Graphs and hypergraphs provide powerful abstractions for modeling interactions among a set of entities of interest and have been attracting a growing interest in the literature thanks to many successful applications in several fields. In particular, they are rapidly expanding in domains such as chemistry and biology, especially in the areas of drug discovery and molecule generation. One of the areas witnessing the fasted growth is the chemical reactions field, where chemical reactions can be naturally encoded as directed hyperedges of a hypergraph. In this paper, we address the chemical reaction classification problem by introducing the notation of a Directed Line Graph (DGL) associated with a given directed hypergraph. On top of it, we build the Directed Line Graph Network (DLGNet), the first spectral-based Graph Neural Network (GNN) expressly designed to operate on a hypergraph via its DLG transformation. The foundation of DLGNet is a novel Hermitian matrix, the Directed Line Graph Laplacian, which compactly encodes the directionality of the interactions taking place within the directed hyperedges of the hypergraph thanks to the DLG representation. The Directed Line Graph Laplacian enjoys many desirable properties, including admitting an eigenvalue decomposition and being positive semidefinite, which make it well-suited for its adoption within a spectral-based GNN. Through extensive experiments on chemical reaction datasets, we show that DGLNet significantly outperforms the existing approaches, achieving on a collection of real-world datasets an average relative-percentage-difference improvement of 33.01%, with a maximum improvement of 37.71%.

From Biased to Unbiased Dynamics: An Infinitesimal Generator Approach

We investigate learning the eigenfunctions of evolution operators for time-reversal invariant stochastic processes, a prime example being the Langevin equation used in molecular dynamics. Many physical or chemical processes described by this equation involve transitions between metastable states separated by high potential barriers that can hardly be crossed during a simulation. To overcome this bottleneck, data are collected via biased simulations that explore the state space more rapidly. We propose a framework for learning from biased simulations rooted in the infinitesimal generator of the process and the associated resolvent operator. We contrast our approach to more common ones based on the transfer operator, showing that it can provably learn the spectral properties of the unbiased system from biased data. In experiments, we highlight the advantages of our method over transfer operator approaches and recent developments based on generator learning, demonstrating its effectiveness in estimating eigenfunctions and eigenvalues. Importantly, we show that even with datasets containing only a few relevant transitions due to sub-optimal biasing, our approach recovers relevant information about the transition mechanism.

Characterizing metastable states with the help of machine learning

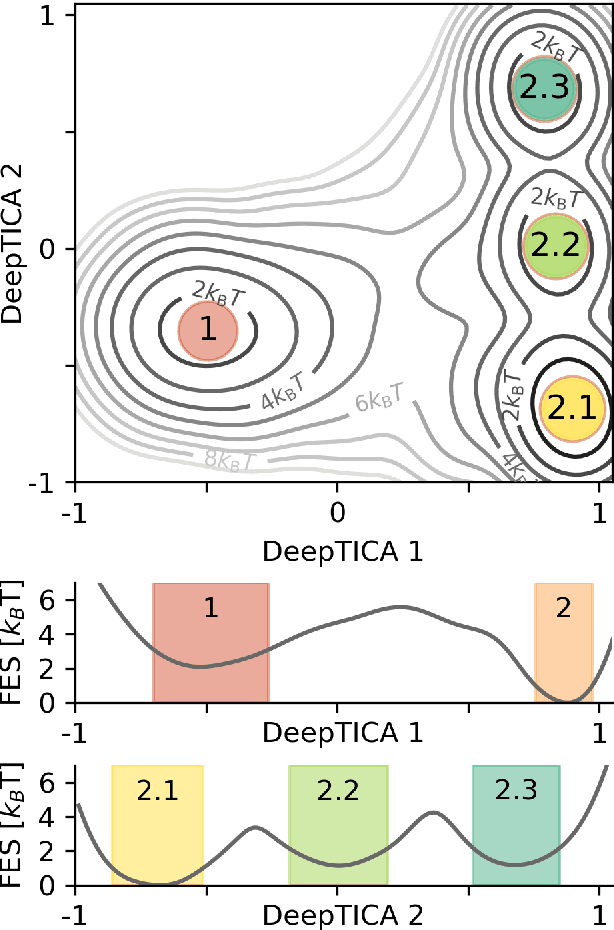
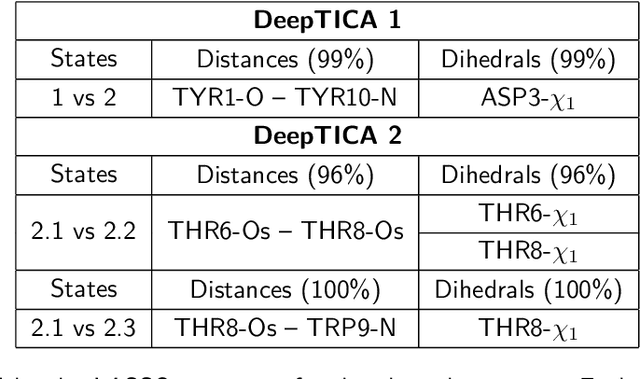
Present-day atomistic simulations generate long trajectories of ever more complex systems. Analyzing these data, discovering metastable states, and uncovering their nature is becoming increasingly challenging. In this paper, we first use the variational approach to conformation dynamics to discover the slowest dynamical modes of the simulations. This allows the different metastable states of the system to be located and organized hierarchically. The physical descriptors that characterize metastable states are discovered by means of a machine learning method. We show in the cases of two proteins, Chignolin and Bovine Pancreatic Trypsin Inhibitor, how such analysis can be effortlessly performed in a matter of seconds. Another strength of our approach is that it can be applied to the analysis of both unbiased and biased simulations.