Classification under strategic adversary manipulation using pessimistic bilevel optimisation

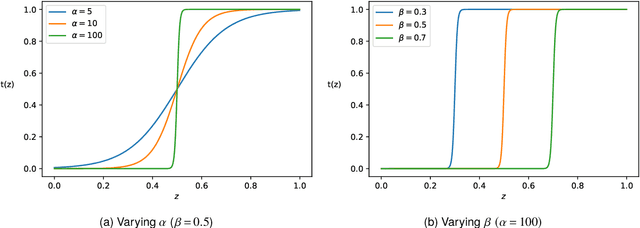
Adversarial machine learning concerns situations in which learners face attacks from active adversaries. Such scenarios arise in applications such as spam email filtering, malware detection and fake-image generation, where security methods must be actively updated to keep up with the ever improving generation of malicious data.We model these interactions between the learner and the adversary as a game and formulate the problem as a pessimistic bilevel optimisation problem with the learner taking the role of the leader. The adversary, modelled as a stochastic data generator, takes the role of the follower, generating data in response to the classifier. While existing models rely on the assumption that the adversary will choose the least costly solution leading to a convex lower-level problem with a unique solution, we present a novel model and solution method which do not make such assumptions. We compare these to the existing approach and see significant improvements in performance suggesting that relaxing these assumptions leads to a more realistic model.

DLGNet: Hyperedge Classification through Directed Line Graphs for Chemical Reactions

Graphs and hypergraphs provide powerful abstractions for modeling interactions among a set of entities of interest and have been attracting a growing interest in the literature thanks to many successful applications in several fields. In particular, they are rapidly expanding in domains such as chemistry and biology, especially in the areas of drug discovery and molecule generation. One of the areas witnessing the fasted growth is the chemical reactions field, where chemical reactions can be naturally encoded as directed hyperedges of a hypergraph. In this paper, we address the chemical reaction classification problem by introducing the notation of a Directed Line Graph (DGL) associated with a given directed hypergraph. On top of it, we build the Directed Line Graph Network (DLGNet), the first spectral-based Graph Neural Network (GNN) expressly designed to operate on a hypergraph via its DLG transformation. The foundation of DLGNet is a novel Hermitian matrix, the Directed Line Graph Laplacian, which compactly encodes the directionality of the interactions taking place within the directed hyperedges of the hypergraph thanks to the DLG representation. The Directed Line Graph Laplacian enjoys many desirable properties, including admitting an eigenvalue decomposition and being positive semidefinite, which make it well-suited for its adoption within a spectral-based GNN. Through extensive experiments on chemical reaction datasets, we show that DGLNet significantly outperforms the existing approaches, achieving on a collection of real-world datasets an average relative-percentage-difference improvement of 33.01%, with a maximum improvement of 37.71%.

Graph Learning in 4D: a Quaternion-valued Laplacian to Enhance Spectral GCNs

We introduce QuaterGCN, a spectral Graph Convolutional Network (GCN) with quaternion-valued weights at whose core lies the Quaternionic Laplacian, a quaternion-valued Laplacian matrix by whose proposal we generalize two widely-used Laplacian matrices: the classical Laplacian (defined for undirected graphs) and the complex-valued Sign-Magnetic Laplacian (proposed to handle digraphs with weights of arbitrary sign). In addition to its generality, our Quaternionic Laplacian is the only Laplacian to completely preserve the topology of a digraph, as it can handle graphs and digraphs containing antiparallel pairs of edges (digons) of different weights without reducing them to a single (directed or undirected) edge as done with other Laplacians. Experimental results show the superior performance of QuaterGCN compared to other state-of-the-art GCNs, particularly in scenarios where the information the digons carry is crucial to successfully address the task at hand.

SigMaNet: One Laplacian to Rule Them All

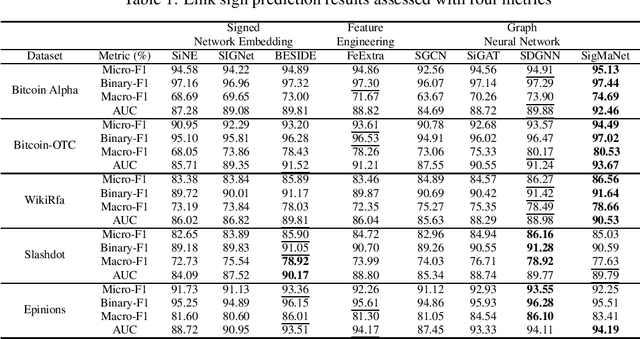
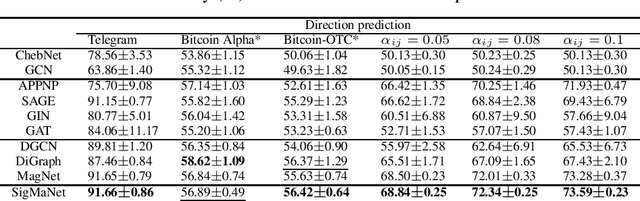
This paper introduces SigMaNet, a generalized Graph Convolutional Network (GCN) capable of handling both undirected and directed graphs with weights not restricted in sign and magnitude. The cornerstone of SigMaNet is the introduction of a generalized Laplacian matrix: the Sign-Magnetic Laplacian ($L^\sigma$). The adoption of such a matrix allows us to bridge a gap in the current literature by extending the theory of spectral GCNs to directed graphs with both positive and negative weights. $L^{\sigma}$ exhibits several desirable properties not enjoyed by the traditional Laplacian matrices on which several state-of-the-art architectures are based. In particular, $L^\sigma$ is completely parameter-free, which is not the case of Laplacian operators such as the Magnetic Laplacian $L^{(q)}$, where the calibration of the parameter q is an essential yet problematic component of the operator. $L^\sigma$ simplifies the approach, while also allowing for a natural interpretation of the signs of the edges in terms of their directions. The versatility of the proposed approach is amply demonstrated experimentally; the proposed network SigMaNet turns out to be competitive in all the tasks we considered, regardless of the graph structure.

Deep learning methods for screening patients' S-ICD implantation eligibility

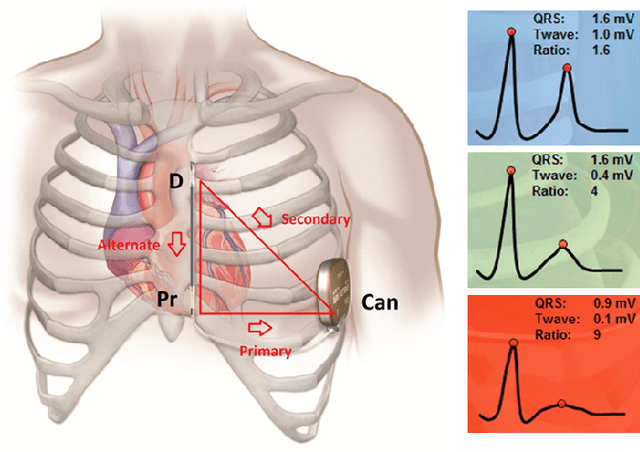
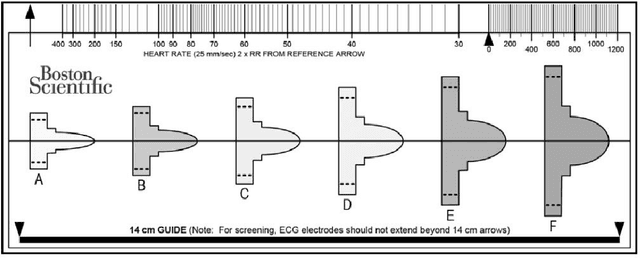
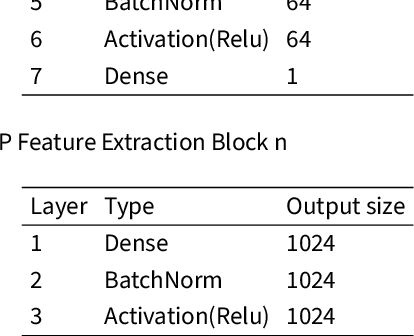
Subcutaneous Implantable Cardioverter-Defibrillators (S-ICDs) are used for prevention of sudden cardiac death triggered by ventricular arrhythmias. T Wave Over Sensing (TWOS) is an inherent risk with S-ICDs which can lead to inappropriate shocks. A major predictor of TWOS is a high T:R ratio (the ratio between the amplitudes of the T and R waves). Currently patients' Electrocardiograms (ECGs) are screened over 10 seconds to measure the T:R ratio, determining the patients' eligibility for S-ICD implantation. Due to temporal variations in the T:R ratio, 10 seconds is not long enough to reliably determine the normal values of a patient's T:R ratio. In this paper, we develop a convolutional neural network (CNN) based model utilising phase space reconstruction matrices to predict T:R ratios from 10-second ECG segments without explicitly locating the R or T waves, thus avoiding the issue of TWOS. This tool can be used to automatically screen patients over a much longer period and provide an in-depth description of the behaviour of the T:R ratio over that period. The tool can also enable much more reliable and descriptive screenings to better assess patients' eligibility for S-ICD implantation.

Infrequent adverse event prediction in low carbon energy production using machine learning

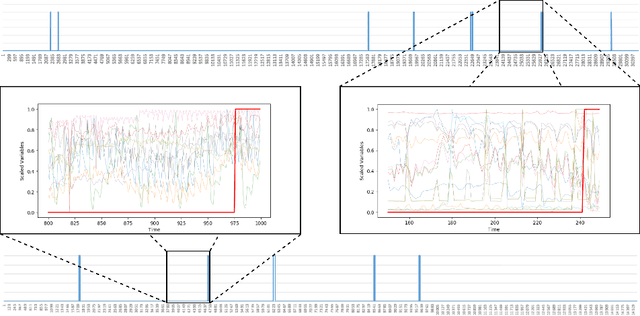
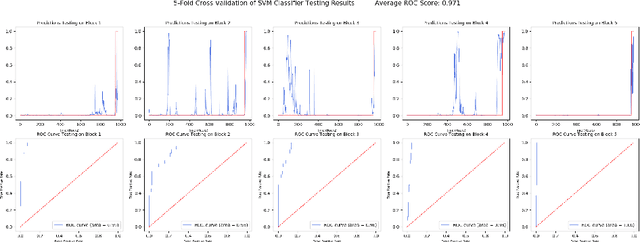
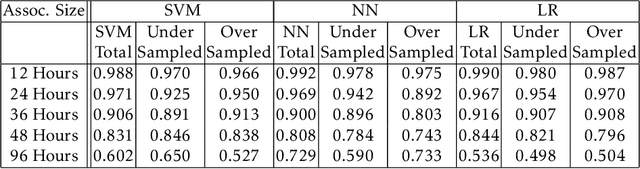
Machine Learning is one of the fastest growing fields in academia. Many industries are aiming to incorporate machine learning tools into their day to day operation. However the keystone of doing so, is recognising when you have a problem which can be solved using machine learning. Adverse event prediction is one such problem. There are a wide range of methods for the production of sustainable energy. In many of which adverse events can occur which can impede energy production and even damage equipment. The two examples of adverse event prediction in sustainable energy production we examine in this paper are foam formation in anaerobic digestion and condenser fouling in steam turbines as used in nuclear power stations. In this paper we will propose a framework for: formalising a classification problem based around adverse event prediction, building predictive maintenance models capable of predicting these events before they occur and testing the reliability of these models.

Bayesian Persuasion with Sequential Games

We study an information-structure design problem (a.k.a. persuasion) with a single sender and multiple receivers with actions of a priori unknown types, independently drawn from action-specific marginal distributions. As in the standard Bayesian persuasion model, the sender has access to additional information regarding the action types, which she can exploit when committing to a (noisy) signaling scheme through which she sends a private signal to each receiver. The novelty of our model is in considering the case where the receivers interact in a sequential game with imperfect information, with utilities depending on the game outcome and the realized action types. After formalizing the notions of ex ante and ex interim persuasiveness (which differ in the time at which the receivers commit to following the sender's signaling scheme), we investigate the continuous optimization problem of computing a signaling scheme which maximizes the sender's expected revenue. We show that computing an optimal ex ante persuasive signaling scheme is NP-hard when there are three or more receivers. In contrast with previous hardness results for ex interim persuasion, we show that, for games with two receivers, an optimal ex ante persuasive signaling scheme can be computed in polynomial time thanks to a novel algorithm based on the ellipsoid method which we propose.

Computing Optimal Coarse Correlated Equilibria in Sequential Games

We investigate the computation of equilibria in extensive-form games where ex ante correlation is possible, focusing on correlated equilibria requiring the least amount of communication between the players and the mediator. Motivated by the hardness results on the computation of normal-form correlated equilibria, we introduce the notion of normal-form coarse correlated equilibrium, extending the definition of coarse correlated equilibrium to sequential games. We show that, in two-player games without chance moves, an optimal (e.g., social welfare maximizing) normal-form coarse correlated equilibrium can be computed in polynomial time, and that in general multi-player games (including two-player games with Chance), the problem is NP-hard. For the former case, we provide a polynomial-time algorithm based on the ellipsoid method and also propose a more practical one, which can be efficiently applied to problems of considerable size. Then, we discuss how our algorithm can be extended to games with Chance and games with more than two players.

Methods for finding leader--follower equilibria with multiple followers

The concept of leader--follower (or Stackelberg) equilibrium plays a central role in a number of real--world applications of game theory. While the case with a single follower has been thoroughly investigated, results with multiple followers are only sporadic and the problem of designing and evaluating computationally tractable equilibrium-finding algorithms is still largely open. In this work, we focus on the fundamental case where multiple followers play a Nash equilibrium once the leader has committed to a strategy---as we illustrate, the corresponding equilibrium finding problem can be easily shown to be $\mathcal{FNP}$--hard and not in Poly--$\mathcal{APX}$ unless $\mathcal{P} = \mathcal{NP}$ and therefore it is one among the hardest problems to solve and approximate. We propose nonconvex mathematical programming formulations and global optimization methods to find both exact and approximate equilibria, as well as a heuristic black box algorithm. All the methods and formulations that we introduce are thoroughly evaluated computationally.