DLGNet: Hyperedge Classification through Directed Line Graphs for Chemical Reactions

Graphs and hypergraphs provide powerful abstractions for modeling interactions among a set of entities of interest and have been attracting a growing interest in the literature thanks to many successful applications in several fields. In particular, they are rapidly expanding in domains such as chemistry and biology, especially in the areas of drug discovery and molecule generation. One of the areas witnessing the fasted growth is the chemical reactions field, where chemical reactions can be naturally encoded as directed hyperedges of a hypergraph. In this paper, we address the chemical reaction classification problem by introducing the notation of a Directed Line Graph (DGL) associated with a given directed hypergraph. On top of it, we build the Directed Line Graph Network (DLGNet), the first spectral-based Graph Neural Network (GNN) expressly designed to operate on a hypergraph via its DLG transformation. The foundation of DLGNet is a novel Hermitian matrix, the Directed Line Graph Laplacian, which compactly encodes the directionality of the interactions taking place within the directed hyperedges of the hypergraph thanks to the DLG representation. The Directed Line Graph Laplacian enjoys many desirable properties, including admitting an eigenvalue decomposition and being positive semidefinite, which make it well-suited for its adoption within a spectral-based GNN. Through extensive experiments on chemical reaction datasets, we show that DGLNet significantly outperforms the existing approaches, achieving on a collection of real-world datasets an average relative-percentage-difference improvement of 33.01%, with a maximum improvement of 37.71%.

Graph Learning in 4D: a Quaternion-valued Laplacian to Enhance Spectral GCNs

We introduce QuaterGCN, a spectral Graph Convolutional Network (GCN) with quaternion-valued weights at whose core lies the Quaternionic Laplacian, a quaternion-valued Laplacian matrix by whose proposal we generalize two widely-used Laplacian matrices: the classical Laplacian (defined for undirected graphs) and the complex-valued Sign-Magnetic Laplacian (proposed to handle digraphs with weights of arbitrary sign). In addition to its generality, our Quaternionic Laplacian is the only Laplacian to completely preserve the topology of a digraph, as it can handle graphs and digraphs containing antiparallel pairs of edges (digons) of different weights without reducing them to a single (directed or undirected) edge as done with other Laplacians. Experimental results show the superior performance of QuaterGCN compared to other state-of-the-art GCNs, particularly in scenarios where the information the digons carry is crucial to successfully address the task at hand.

SigMaNet: One Laplacian to Rule Them All

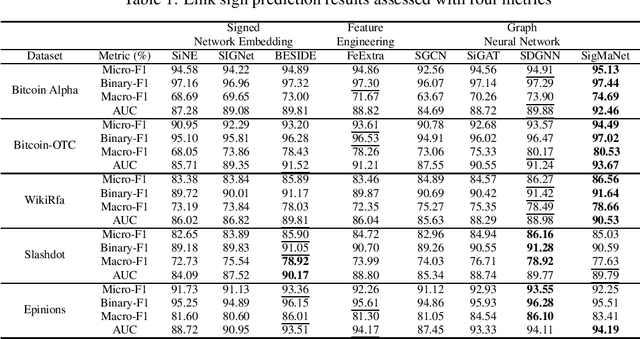
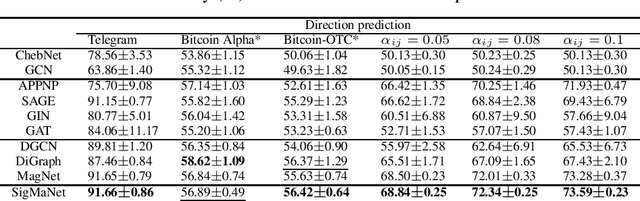
This paper introduces SigMaNet, a generalized Graph Convolutional Network (GCN) capable of handling both undirected and directed graphs with weights not restricted in sign and magnitude. The cornerstone of SigMaNet is the introduction of a generalized Laplacian matrix: the Sign-Magnetic Laplacian ($L^\sigma$). The adoption of such a matrix allows us to bridge a gap in the current literature by extending the theory of spectral GCNs to directed graphs with both positive and negative weights. $L^{\sigma}$ exhibits several desirable properties not enjoyed by the traditional Laplacian matrices on which several state-of-the-art architectures are based. In particular, $L^\sigma$ is completely parameter-free, which is not the case of Laplacian operators such as the Magnetic Laplacian $L^{(q)}$, where the calibration of the parameter q is an essential yet problematic component of the operator. $L^\sigma$ simplifies the approach, while also allowing for a natural interpretation of the signs of the edges in terms of their directions. The versatility of the proposed approach is amply demonstrated experimentally; the proposed network SigMaNet turns out to be competitive in all the tasks we considered, regardless of the graph structure.

ANDREAS: Artificial intelligence traiNing scheDuler foR accElerAted resource clusterS

Artificial Intelligence (AI) and Deep Learning (DL) algorithms are currently applied to a wide range of products and solutions. DL training jobs are highly resource demanding and they experience great benefits when exploiting AI accelerators (e.g., GPUs). However, the effective management of GPU-powered clusters comes with great challenges. Among these, efficient scheduling and resource allocation solutions are crucial to maximize performance and minimize Data Centers operational costs. In this paper we propose ANDREAS, an advanced scheduling solution that tackles these problems jointly, aiming at optimizing DL training runtime workloads and their energy consumption in accelerated clusters. Experiments based on simulation demostrate that we can achieve a cost reduction between 30 and 62% on average with respect to first-principle methods while the validation on a real cluster shows a worst case deviation below 13% between actual and predicted costs, proving the effectiveness of ANDREAS solution in practical scenarios.

Listening to the city, attentively: A Spatio-Temporal Attention Boosted Autoencoder for the Short-Term Flow Prediction Problem

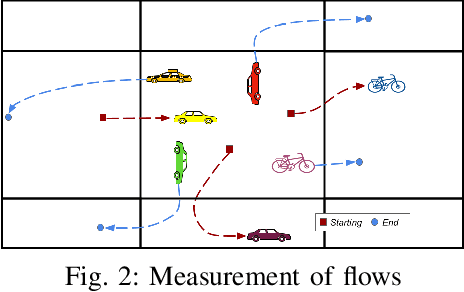
In recent years, the importance of studying traffic flows and making predictions on alternative mobility (sharing services) has become increasingly important, as accurate and timely information on the travel flow is important for the successful implementation of systems that increase the quality of sharing services. This need has been accentuated by the current health crisis that requires alternative transport mobility such as electric bike and electric scooter sharing. Considering the new approaches in the world of deep learning and the difficulty due to the strong spatial and temporal dependence of this problem, we propose a framework, called STREED-Net, with multi-attention (Spatial and Temporal) able to better mining the high-level spatial and temporal features. We conduct experiments on three real datasets to predict the Inflow and Outflow of the different regions into which the city has been divided. The results indicate that the proposed STREED-Net model improves the state-of-the-art for this problem.