SigMaNet: One Laplacian to Rule Them All
Paper and Code
May 26, 2022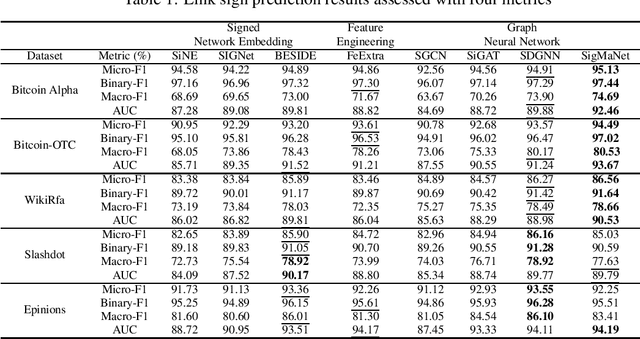

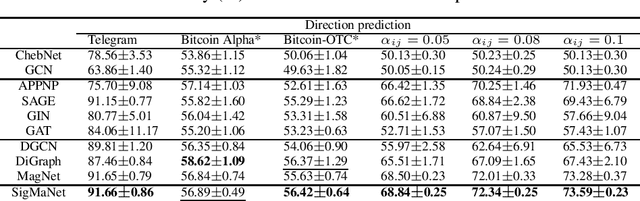

This paper introduces SigMaNet, a generalized Graph Convolutional Network (GCN) capable of handling both undirected and directed graphs with weights not restricted in sign and magnitude. The cornerstone of SigMaNet is the introduction of a generalized Laplacian matrix: the Sign-Magnetic Laplacian ($L^\sigma$). The adoption of such a matrix allows us to bridge a gap in the current literature by extending the theory of spectral GCNs to directed graphs with both positive and negative weights. $L^{\sigma}$ exhibits several desirable properties not enjoyed by the traditional Laplacian matrices on which several state-of-the-art architectures are based. In particular, $L^\sigma$ is completely parameter-free, which is not the case of Laplacian operators such as the Magnetic Laplacian $L^{(q)}$, where the calibration of the parameter q is an essential yet problematic component of the operator. $L^\sigma$ simplifies the approach, while also allowing for a natural interpretation of the signs of the edges in terms of their directions. The versatility of the proposed approach is amply demonstrated experimentally; the proposed network SigMaNet turns out to be competitive in all the tasks we considered, regardless of the graph structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge