Maps from Motion (MfM): Generating 2D Semantic Maps from Sparse Multi-view Images

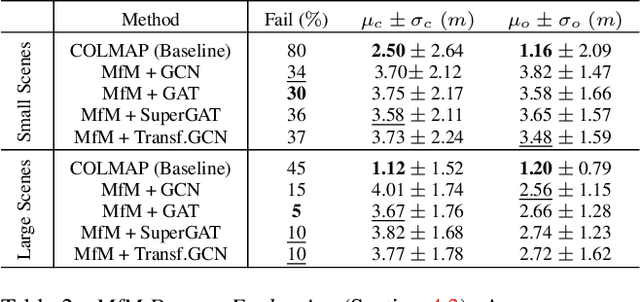
World-wide detailed 2D maps require enormous collective efforts. OpenStreetMap is the result of 11 million registered users manually annotating the GPS location of over 1.75 billion entries, including distinctive landmarks and common urban objects. At the same time, manual annotations can include errors and are slow to update, limiting the map's accuracy. Maps from Motion (MfM) is a step forward to automatize such time-consuming map making procedure by computing 2D maps of semantic objects directly from a collection of uncalibrated multi-view images. From each image, we extract a set of object detections, and estimate their spatial arrangement in a top-down local map centered in the reference frame of the camera that captured the image. Aligning these local maps is not a trivial problem, since they provide incomplete, noisy fragments of the scene, and matching detections across them is unreliable because of the presence of repeated pattern and the limited appearance variability of urban objects. We address this with a novel graph-based framework, that encodes the spatial and semantic distribution of the objects detected in each image, and learns how to combine them to predict the objects' poses in a global reference system, while taking into account all possible detection matches and preserving the topology observed in each image. Despite the complexity of the problem, our best model achieves global 2D registration with an average accuracy within 4 meters (i.e., below GPS accuracy) even on sparse sequences with strong viewpoint change, on which COLMAP has an 80% failure rate. We provide extensive evaluation on synthetic and real-world data, showing how the method obtains a solution even in scenarios where standard optimization techniques fail.

Re-assembling the past: The RePAIR dataset and benchmark for real world 2D and 3D puzzle solving

This paper proposes the RePAIR dataset that represents a challenging benchmark to test modern computational and data driven methods for puzzle-solving and reassembly tasks. Our dataset has unique properties that are uncommon to current benchmarks for 2D and 3D puzzle solving. The fragments and fractures are realistic, caused by a collapse of a fresco during a World War II bombing at the Pompeii archaeological park. The fragments are also eroded and have missing pieces with irregular shapes and different dimensions, challenging further the reassembly algorithms. The dataset is multi-modal providing high resolution images with characteristic pictorial elements, detailed 3D scans of the fragments and meta-data annotated by the archaeologists. Ground truth has been generated through several years of unceasing fieldwork, including the excavation and cleaning of each fragment, followed by manual puzzle solving by archaeologists of a subset of approx. 1000 pieces among the 16000 available. After digitizing all the fragments in 3D, a benchmark was prepared to challenge current reassembly and puzzle-solving methods that often solve more simplistic synthetic scenarios. The tested baselines show that there clearly exists a gap to fill in solving this computationally complex problem.

DLGNet: Hyperedge Classification through Directed Line Graphs for Chemical Reactions

Graphs and hypergraphs provide powerful abstractions for modeling interactions among a set of entities of interest and have been attracting a growing interest in the literature thanks to many successful applications in several fields. In particular, they are rapidly expanding in domains such as chemistry and biology, especially in the areas of drug discovery and molecule generation. One of the areas witnessing the fasted growth is the chemical reactions field, where chemical reactions can be naturally encoded as directed hyperedges of a hypergraph. In this paper, we address the chemical reaction classification problem by introducing the notation of a Directed Line Graph (DGL) associated with a given directed hypergraph. On top of it, we build the Directed Line Graph Network (DLGNet), the first spectral-based Graph Neural Network (GNN) expressly designed to operate on a hypergraph via its DLG transformation. The foundation of DLGNet is a novel Hermitian matrix, the Directed Line Graph Laplacian, which compactly encodes the directionality of the interactions taking place within the directed hyperedges of the hypergraph thanks to the DLG representation. The Directed Line Graph Laplacian enjoys many desirable properties, including admitting an eigenvalue decomposition and being positive semidefinite, which make it well-suited for its adoption within a spectral-based GNN. Through extensive experiments on chemical reaction datasets, we show that DGLNet significantly outperforms the existing approaches, achieving on a collection of real-world datasets an average relative-percentage-difference improvement of 33.01%, with a maximum improvement of 37.71%.

DiffAssemble: A Unified Graph-Diffusion Model for 2D and 3D Reassembly

Reassembly tasks play a fundamental role in many fields and multiple approaches exist to solve specific reassembly problems. In this context, we posit that a general unified model can effectively address them all, irrespective of the input data type (images, 3D, etc.). We introduce DiffAssemble, a Graph Neural Network (GNN)-based architecture that learns to solve reassembly tasks using a diffusion model formulation. Our method treats the elements of a set, whether pieces of 2D patch or 3D object fragments, as nodes of a spatial graph. Training is performed by introducing noise into the position and rotation of the elements and iteratively denoising them to reconstruct the coherent initial pose. DiffAssemble achieves state-of-the-art (SOTA) results in most 2D and 3D reassembly tasks and is the first learning-based approach that solves 2D puzzles for both rotation and translation. Furthermore, we highlight its remarkable reduction in run-time, performing 11 times faster than the quickest optimization-based method for puzzle solving. Code available at https://github.com/IIT-PAVIS/DiffAssemble

Graph Learning in 4D: a Quaternion-valued Laplacian to Enhance Spectral GCNs

We introduce QuaterGCN, a spectral Graph Convolutional Network (GCN) with quaternion-valued weights at whose core lies the Quaternionic Laplacian, a quaternion-valued Laplacian matrix by whose proposal we generalize two widely-used Laplacian matrices: the classical Laplacian (defined for undirected graphs) and the complex-valued Sign-Magnetic Laplacian (proposed to handle digraphs with weights of arbitrary sign). In addition to its generality, our Quaternionic Laplacian is the only Laplacian to completely preserve the topology of a digraph, as it can handle graphs and digraphs containing antiparallel pairs of edges (digons) of different weights without reducing them to a single (directed or undirected) edge as done with other Laplacians. Experimental results show the superior performance of QuaterGCN compared to other state-of-the-art GCNs, particularly in scenarios where the information the digons carry is crucial to successfully address the task at hand.

SigMaNet: One Laplacian to Rule Them All

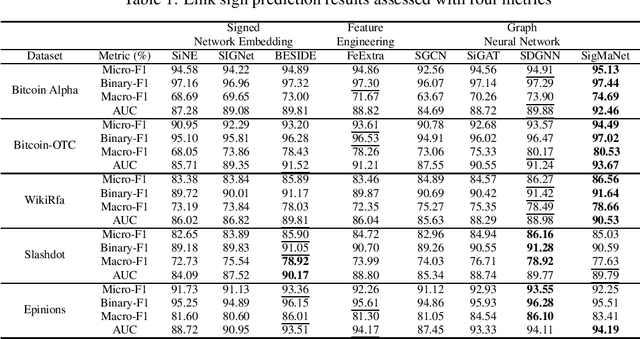
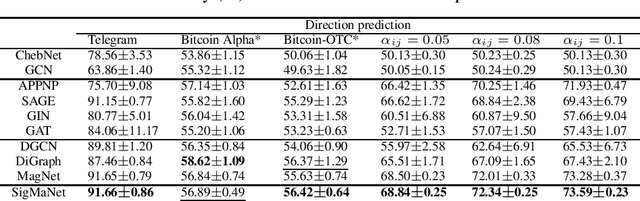
This paper introduces SigMaNet, a generalized Graph Convolutional Network (GCN) capable of handling both undirected and directed graphs with weights not restricted in sign and magnitude. The cornerstone of SigMaNet is the introduction of a generalized Laplacian matrix: the Sign-Magnetic Laplacian ($L^\sigma$). The adoption of such a matrix allows us to bridge a gap in the current literature by extending the theory of spectral GCNs to directed graphs with both positive and negative weights. $L^{\sigma}$ exhibits several desirable properties not enjoyed by the traditional Laplacian matrices on which several state-of-the-art architectures are based. In particular, $L^\sigma$ is completely parameter-free, which is not the case of Laplacian operators such as the Magnetic Laplacian $L^{(q)}$, where the calibration of the parameter q is an essential yet problematic component of the operator. $L^\sigma$ simplifies the approach, while also allowing for a natural interpretation of the signs of the edges in terms of their directions. The versatility of the proposed approach is amply demonstrated experimentally; the proposed network SigMaNet turns out to be competitive in all the tasks we considered, regardless of the graph structure.

Listening to the city, attentively: A Spatio-Temporal Attention Boosted Autoencoder for the Short-Term Flow Prediction Problem

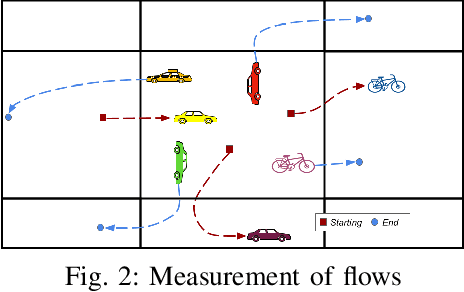
In recent years, the importance of studying traffic flows and making predictions on alternative mobility (sharing services) has become increasingly important, as accurate and timely information on the travel flow is important for the successful implementation of systems that increase the quality of sharing services. This need has been accentuated by the current health crisis that requires alternative transport mobility such as electric bike and electric scooter sharing. Considering the new approaches in the world of deep learning and the difficulty due to the strong spatial and temporal dependence of this problem, we propose a framework, called STREED-Net, with multi-attention (Spatial and Temporal) able to better mining the high-level spatial and temporal features. We conduct experiments on three real datasets to predict the Inflow and Outflow of the different regions into which the city has been divided. The results indicate that the proposed STREED-Net model improves the state-of-the-art for this problem.