Large sample analysis of the median heuristic
Paper and Code
Oct 30, 2018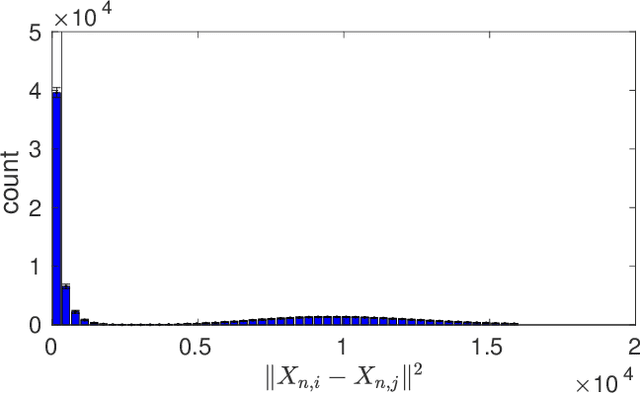
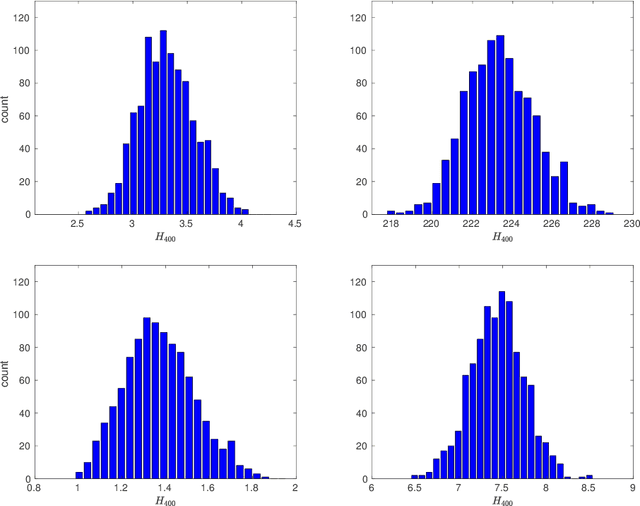
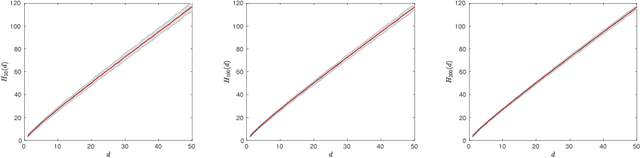
In kernel methods, the median heuristic has been widely used as a way of setting the bandwidth of RBF kernels. While its empirical performances make it a safe choice under many circumstances, there is little theoretical understanding of why this is the case. Our aim in this paper is to advance our understanding of the median heuristic by focusing on the setting of kernel two-sample test. We collect new findings that may be of interest for both theoreticians and practitioners. In theory, we provide a convergence analysis that shows the asymptotic normality of the bandwidth chosen by the median heuristic in the setting of kernel two-sample test. Systematic empirical investigations are also conducted in simple settings, comparing the performances based on the bandwidths chosen by the median heuristic and those by the maximization of test power.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge