Variable Selection for Comparing High-dimensional Time-Series Data

Given a pair of multivariate time-series data of the same length and dimensions, an approach is proposed to select variables and time intervals where the two series are significantly different. In applications where one time series is an output from a computationally expensive simulator, the approach may be used for validating the simulator against real data, for comparing the outputs of two simulators, and for validating a machine learning-based emulator against the simulator. With the proposed approach, the entire time interval is split into multiple subintervals, and on each subinterval, the two sample sets are compared to select variables that distinguish their distributions and a two-sample test is performed. The validity and limitations of the proposed approach are investigated in synthetic data experiments. Its usefulness is demonstrated in an application with a particle-based fluid simulator, where a deep neural network model is compared against the simulator, and in an application with a microscopic traffic simulator, where the effects of changing the simulator's parameters on traffic flows are analysed.

Variable Selection in Maximum Mean Discrepancy for Interpretable Distribution Comparison

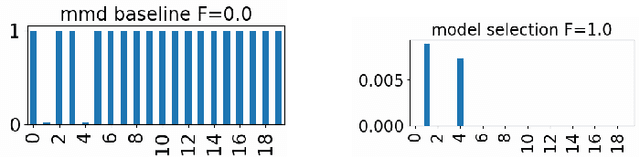
Two-sample testing decides whether two datasets are generated from the same distribution. This paper studies variable selection for two-sample testing, the task being to identify the variables (or dimensions) responsible for the discrepancies between the two distributions. This task is relevant to many problems of pattern analysis and machine learning, such as dataset shift adaptation, causal inference and model validation. Our approach is based on a two-sample test based on the Maximum Mean Discrepancy (MMD). We optimise the Automatic Relevance Detection (ARD) weights defined for individual variables to maximise the power of the MMD-based test. For this optimisation, we introduce sparse regularisation and propose two methods for dealing with the issue of selecting an appropriate regularisation parameter. One method determines the regularisation parameter in a data-driven way, and the other aggregates the results of different regularisation parameters. We confirm the validity of the proposed methods by systematic comparisons with baseline methods, and demonstrate their usefulness in exploratory analysis of high-dimensional traffic simulation data. Preliminary theoretical analyses are also provided, including a rigorous definition of variable selection for two-sample testing.