A Sparsity Principle for Partially Observable Causal Representation Learning

Causal representation learning aims at identifying high-level causal variables from perceptual data. Most methods assume that all latent causal variables are captured in the high-dimensional observations. We instead consider a partially observed setting, in which each measurement only provides information about a subset of the underlying causal state. Prior work has studied this setting with multiple domains or views, each depending on a fixed subset of latents. Here, we focus on learning from unpaired observations from a dataset with an instance-dependent partial observability pattern. Our main contribution is to establish two identifiability results for this setting: one for linear mixing functions without parametric assumptions on the underlying causal model, and one for piecewise linear mixing functions with Gaussian latent causal variables. Based on these insights, we propose two methods for estimating the underlying causal variables by enforcing sparsity in the inferred representation. Experiments on different simulated datasets and established benchmarks highlight the effectiveness of our approach in recovering the ground-truth latents.

Multi-View Causal Representation Learning with Partial Observability

We present a unified framework for studying the identifiability of representations learned from simultaneously observed views, such as different data modalities. We allow a partially observed setting in which each view constitutes a nonlinear mixture of a subset of underlying latent variables, which can be causally related. We prove that the information shared across all subsets of any number of views can be learned up to a smooth bijection using contrastive learning and a single encoder per view. We also provide graphical criteria indicating which latent variables can be identified through a simple set of rules, which we refer to as identifiability algebra. Our general framework and theoretical results unify and extend several previous works on multi-view nonlinear ICA, disentanglement, and causal representation learning. We experimentally validate our claims on numerical, image, and multi-modal data sets. Further, we demonstrate that the performance of prior methods is recovered in different special cases of our setup. Overall, we find that access to multiple partial views enables us to identify a more fine-grained representation, under the generally milder assumption of partial observability.

On the Sparse DAG Structure Learning Based on Adaptive Lasso

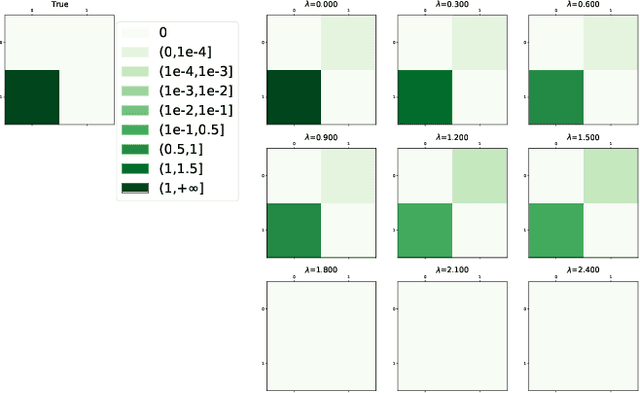
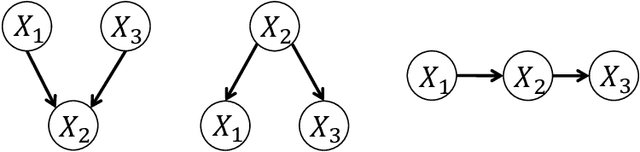
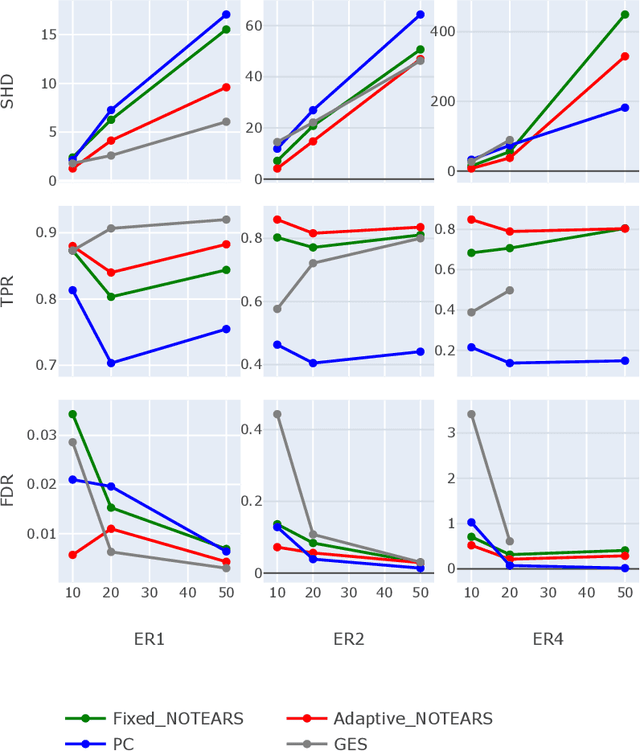
Learning the underlying casual structure, represented by Directed Acyclic Graphs (DAGs), of concerned events from fully-observational data is a crucial part of causal reasoning, but it is challenging due to the combinatorial and large search space. A recent flurry of developments recast this combinatorial problem into a continuous optimization problem by leveraging an algebraic equality characterization of acyclicity. However, these methods suffer from the fixed-threshold step after optimization, which is not a flexible and systematic way to rule out the cycle-inducing edges or false discoveries edges with small values caused by numerical precision. In this paper, we develop a data-driven DAG structure learning method without the predefined threshold, called adaptive NOTEARS [30], achieved by applying adaptive penalty levels to each parameters in the regularization term. We show that adaptive NOTEARS enjoys the oracle properties under some specific conditions. Furthermore, simulation experimental results validate the effectiveness of our method, without setting any gap of edges weights around zero.