On the Sparse DAG Structure Learning Based on Adaptive Lasso

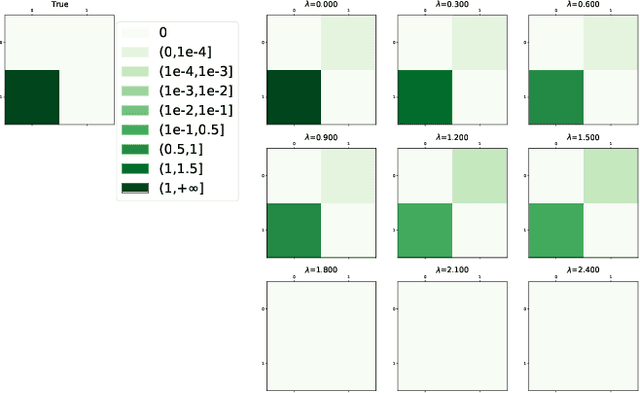
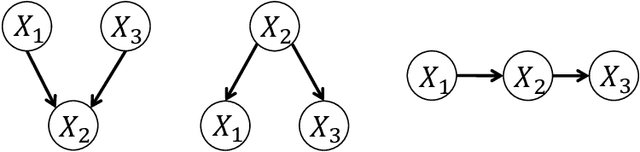
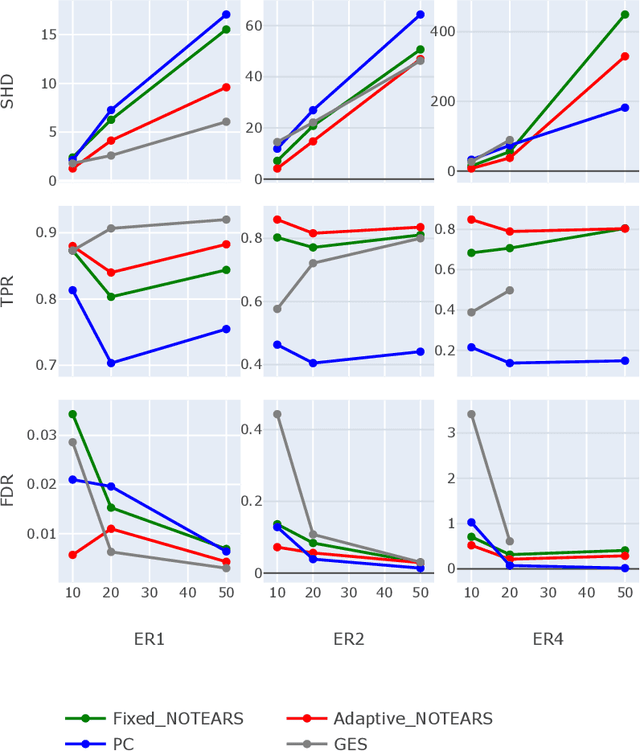
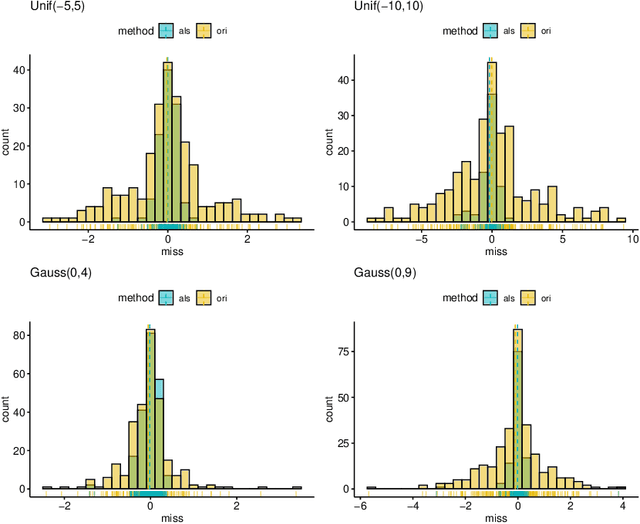
Learning the underlying casual structure, represented by Directed Acyclic Graphs (DAGs), of concerned events from fully-observational data is a crucial part of causal reasoning, but it is challenging due to the combinatorial and large search space. A recent flurry of developments recast this combinatorial problem into a continuous optimization problem by leveraging an algebraic equality characterization of acyclicity. However, these methods suffer from the fixed-threshold step after optimization, which is not a flexible and systematic way to rule out the cycle-inducing edges or false discoveries edges with small values caused by numerical precision. In this paper, we develop a data-driven DAG structure learning method without the predefined threshold, called adaptive NOTEARS [30], achieved by applying adaptive penalty levels to each parameters in the regularization term. We show that adaptive NOTEARS enjoys the oracle properties under some specific conditions. Furthermore, simulation experimental results validate the effectiveness of our method, without setting any gap of edges weights around zero.