From Logits to Hierarchies: Hierarchical Clustering made Simple

The structure of many real-world datasets is intrinsically hierarchical, making the modeling of such hierarchies a critical objective in both unsupervised and supervised machine learning. Recently, novel approaches for hierarchical clustering with deep architectures have been proposed. In this work, we take a critical perspective on this line of research and demonstrate that many approaches exhibit major limitations when applied to realistic datasets, partly due to their high computational complexity. In particular, we show that a lightweight procedure implemented on top of pre-trained non-hierarchical clustering models outperforms models designed specifically for hierarchical clustering. Our proposed approach is computationally efficient and applicable to any pre-trained clustering model that outputs logits, without requiring any fine-tuning. To highlight the generality of our findings, we illustrate how our method can also be applied in a supervised setup, recovering meaningful hierarchies from a pre-trained ImageNet classifier.

Anomaly Detection by Context Contrasting

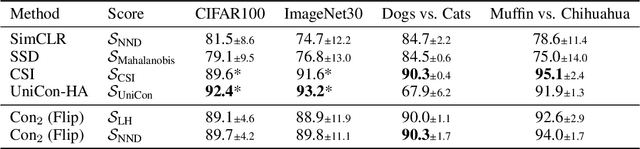
Anomaly Detection focuses on identifying samples that deviate from the norm. When working with high-dimensional data such as images, a crucial requirement for detecting anomalous patterns is learning lower-dimensional representations that capture normal concepts seen during training. Recent advances in self-supervised learning have shown great promise in this regard. However, many of the most successful self-supervised anomaly detection methods assume prior knowledge about the structure of anomalies and leverage synthetic anomalies during training. Yet, in many real-world applications, we do not know what to expect from unseen data, and we can solely leverage knowledge about normal data. In this work, we propose Con2, which addresses this problem by setting normal training data into distinct contexts while preserving its normal properties, letting us observe the data from different perspectives. Unseen normal data consequently adheres to learned context representations while anomalies fail to do so, letting us detect them without any knowledge about anomalies during training. Our experiments demonstrate that our approach achieves state-of-the-art performance on various benchmarks while exhibiting superior performance in a more realistic healthcare setting, where knowledge about potential anomalies is often scarce.

Tree Variational Autoencoders

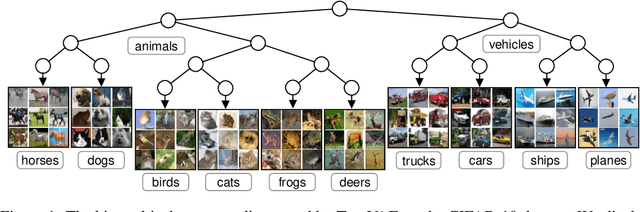
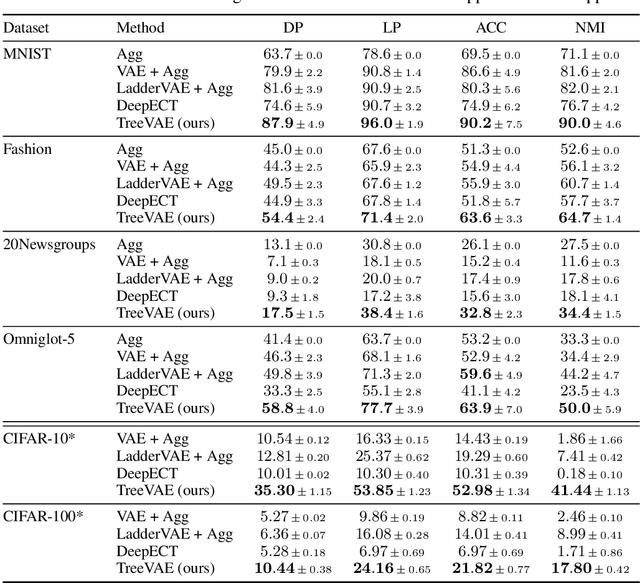
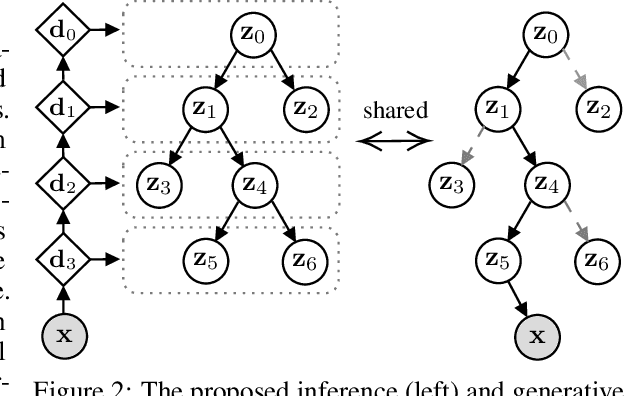
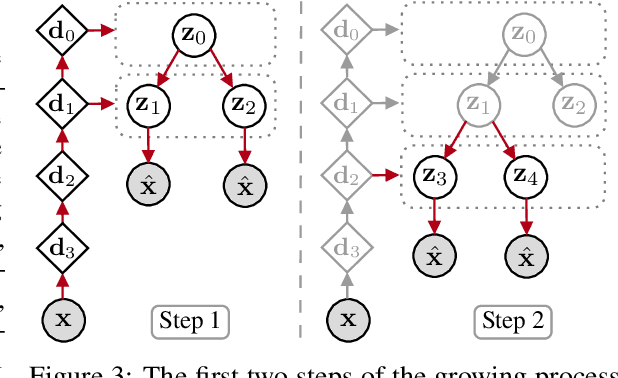
We propose a new generative hierarchical clustering model that learns a flexible tree-based posterior distribution over latent variables. The proposed Tree Variational Autoencoder (TreeVAE) hierarchically divides samples according to their intrinsic characteristics, shedding light on hidden structure in the data. It adapts its architecture to discover the optimal tree for encoding dependencies between latent variables. The proposed tree-based generative architecture permits lightweight conditional inference and improves generative performance by utilizing specialized leaf decoders. We show that TreeVAE uncovers underlying clusters in the data and finds meaningful hierarchical relations between the different groups on a variety of datasets, including real-world imaging data. We present empirically that TreeVAE provides a more competitive log-likelihood lower bound than the sequential counterparts. Finally, due to its generative nature, TreeVAE is able to generate new samples from the discovered clusters via conditional sampling.

Differentiable Random Partition Models

Partitioning a set of elements into an unknown number of mutually exclusive subsets is essential in many machine learning problems. However, assigning elements, such as samples in a dataset or neurons in a network layer, to an unknown and discrete number of subsets is inherently non-differentiable, prohibiting end-to-end gradient-based optimization of parameters. We overcome this limitation by proposing a novel two-step method for inferring partitions, which allows its usage in variational inference tasks. This new approach enables reparameterized gradients with respect to the parameters of the new random partition model. Our method works by inferring the number of elements per subset and, second, by filling these subsets in a learned order. We highlight the versatility of our general-purpose approach on three different challenging experiments: variational clustering, inference of shared and independent generative factors under weak supervision, and multitask learning.

Interpretable Anomaly Detection in Echocardiograms with Dynamic Variational Trajectory Models

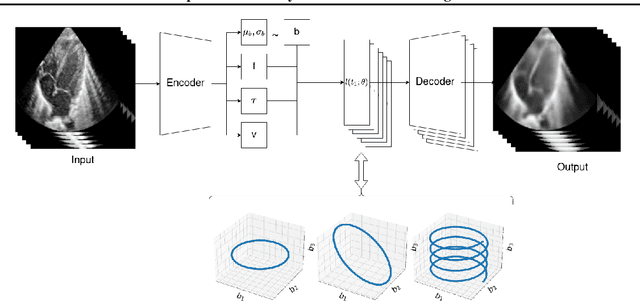
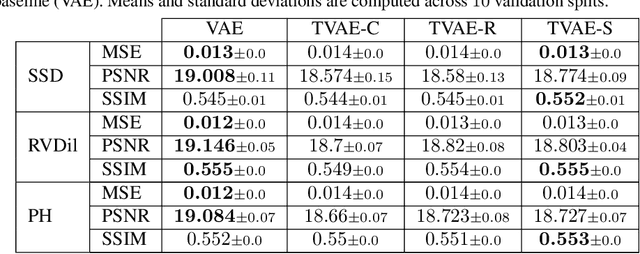
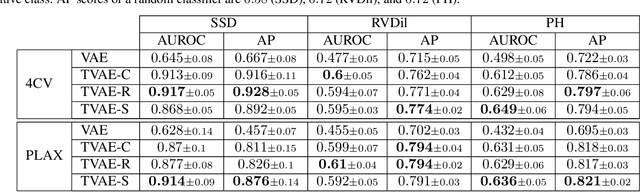
We propose a novel anomaly detection method for echocardiogram videos. The introduced method takes advantage of the periodic nature of the heart cycle to learn different variants of a variational latent trajectory model (TVAE). The models are trained on the healthy samples of an in-house dataset of infant echocardiogram videos consisting of multiple chamber views to learn a normative prior of the healthy population. During inference, maximum a posteriori (MAP) based anomaly detection is performed to detect out-of-distribution samples in our dataset. The proposed method reliably identifies severe congenital heart defects, such as Ebstein's Anomaly or Shonecomplex. Moreover, it achieves superior performance over MAP-based anomaly detection with standard variational autoencoders on the task of detecting pulmonary hypertension and right ventricular dilation. Finally, we demonstrate that the proposed method provides interpretable explanations of its output through heatmaps which highlight the regions corresponding to anomalous heart structures.

Continuous Relaxation For The Multivariate Non-Central Hypergeometric Distribution

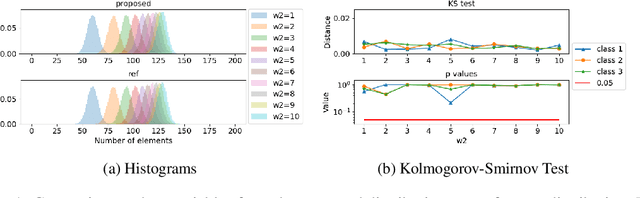
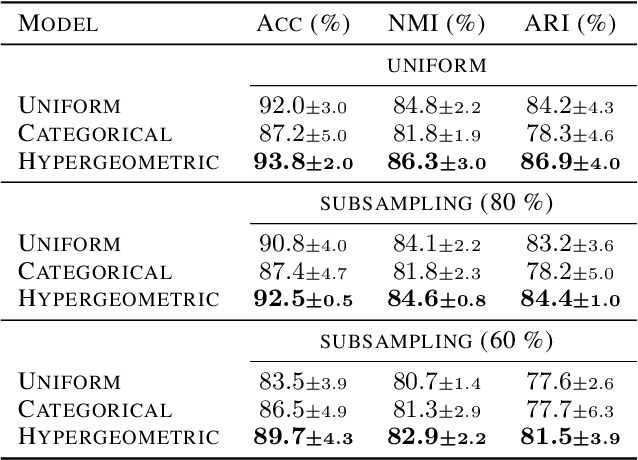
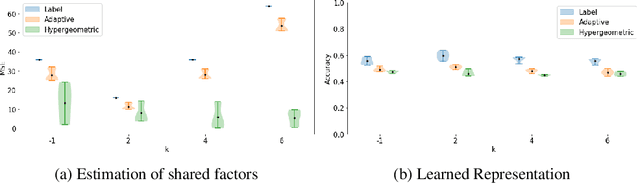
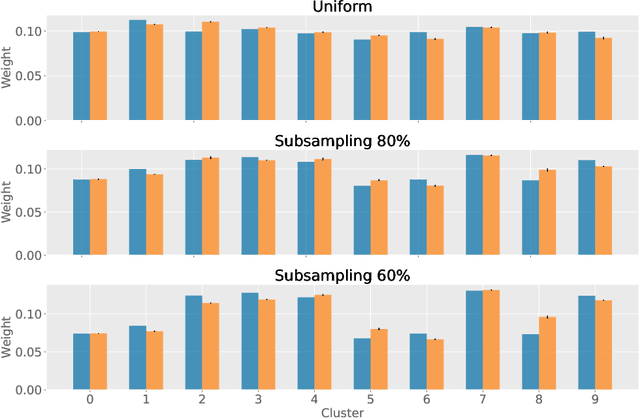
Partitioning a set of elements into a given number of groups of a priori unknown sizes is an important task in many applications. Due to hard constraints, it is a non-differentiable problem which prohibits its direct use in modern machine learning frameworks. Hence, previous works mostly fall back on suboptimal heuristics or simplified assumptions. The multivariate hypergeometric distribution offers a probabilistic formulation of how to distribute a given number of samples across multiple groups. Unfortunately, as a discrete probability distribution, it neither is differentiable. In this work, we propose a continuous relaxation for the multivariate non-central hypergeometric distribution. We introduce an efficient and numerically stable sampling procedure. This enables reparameterized gradients for the hypergeometric distribution and its integration into automatic differentiation frameworks. We highlight the applicability and usability of the proposed formulation on two different common machine learning tasks.