Weakly-Supervised Multimodal Learning on MIMIC-CXR

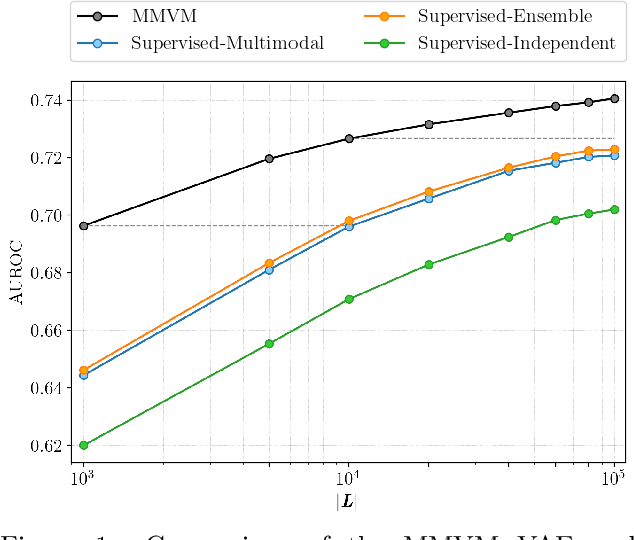
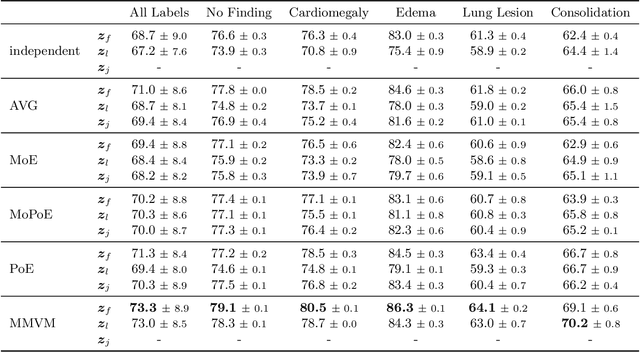
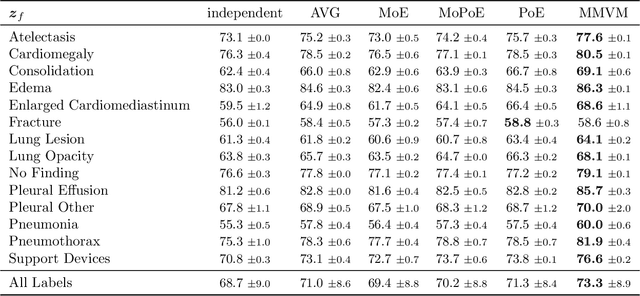
Multimodal data integration and label scarcity pose significant challenges for machine learning in medical settings. To address these issues, we conduct an in-depth evaluation of the newly proposed Multimodal Variational Mixture-of-Experts (MMVM) VAE on the challenging MIMIC-CXR dataset. Our analysis demonstrates that the MMVM VAE consistently outperforms other multimodal VAEs and fully supervised approaches, highlighting its strong potential for real-world medical applications.

Anomaly Detection by Context Contrasting

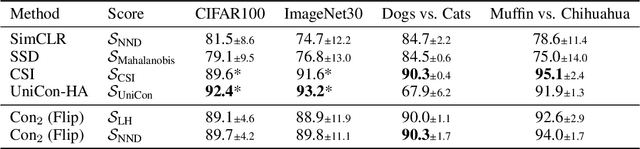
Anomaly Detection focuses on identifying samples that deviate from the norm. When working with high-dimensional data such as images, a crucial requirement for detecting anomalous patterns is learning lower-dimensional representations that capture normal concepts seen during training. Recent advances in self-supervised learning have shown great promise in this regard. However, many of the most successful self-supervised anomaly detection methods assume prior knowledge about the structure of anomalies and leverage synthetic anomalies during training. Yet, in many real-world applications, we do not know what to expect from unseen data, and we can solely leverage knowledge about normal data. In this work, we propose Con2, which addresses this problem by setting normal training data into distinct contexts while preserving its normal properties, letting us observe the data from different perspectives. Unseen normal data consequently adheres to learned context representations while anomalies fail to do so, letting us detect them without any knowledge about anomalies during training. Our experiments demonstrate that our approach achieves state-of-the-art performance on various benchmarks while exhibiting superior performance in a more realistic healthcare setting, where knowledge about potential anomalies is often scarce.

Unity by Diversity: Improved Representation Learning in Multimodal VAEs

Variational Autoencoders for multimodal data hold promise for many tasks in data analysis, such as representation learning, conditional generation, and imputation. Current architectures either share the encoder output, decoder input, or both across modalities to learn a shared representation. Such architectures impose hard constraints on the model. In this work, we show that a better latent representation can be obtained by replacing these hard constraints with a soft constraint. We propose a new mixture-of-experts prior, softly guiding each modality's latent representation towards a shared aggregate posterior. This approach results in a superior latent representation and allows each encoding to preserve information from its uncompressed original features better. In extensive experiments on multiple benchmark datasets and a challenging real-world neuroscience data set, we show improved learned latent representations and imputation of missing data modalities compared to existing methods.

M-mode Based Prediction of Ejection Fraction using Echocardiograms

Early detection of cardiac dysfunction through routine screening is vital for diagnosing cardiovascular diseases. An important metric of cardiac function is the left ventricular ejection fraction (EF), where lower EF is associated with cardiomyopathy. Echocardiography is a popular diagnostic tool in cardiology, with ultrasound being a low-cost, real-time, and non-ionizing technology. However, human assessment of echocardiograms for calculating EF is time-consuming and expertise-demanding, raising the need for an automated approach. In this work, we propose using the M(otion)-mode of echocardiograms for estimating the EF and classifying cardiomyopathy. We generate multiple artificial M-mode images from a single echocardiogram and combine them using off-the-shelf model architectures. Additionally, we extend contrastive learning (CL) to cardiac imaging to learn meaningful representations from exploiting structures in unlabeled data allowing the model to achieve high accuracy, even with limited annotations. Our experiments show that the supervised setting converges with only ten modes and is comparable to the baseline method while bypassing its cumbersome training process and being computationally much more efficient. Furthermore, CL using M-mode images is helpful for limited data scenarios, such as having labels for only 200 patients, which is common in medical applications.

Differentiable Random Partition Models

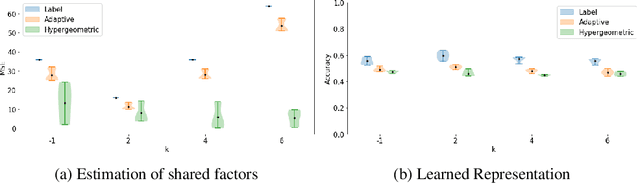
Partitioning a set of elements into an unknown number of mutually exclusive subsets is essential in many machine learning problems. However, assigning elements, such as samples in a dataset or neurons in a network layer, to an unknown and discrete number of subsets is inherently non-differentiable, prohibiting end-to-end gradient-based optimization of parameters. We overcome this limitation by proposing a novel two-step method for inferring partitions, which allows its usage in variational inference tasks. This new approach enables reparameterized gradients with respect to the parameters of the new random partition model. Our method works by inferring the number of elements per subset and, second, by filling these subsets in a learned order. We highlight the versatility of our general-purpose approach on three different challenging experiments: variational clustering, inference of shared and independent generative factors under weak supervision, and multitask learning.

Continuous Relaxation For The Multivariate Non-Central Hypergeometric Distribution

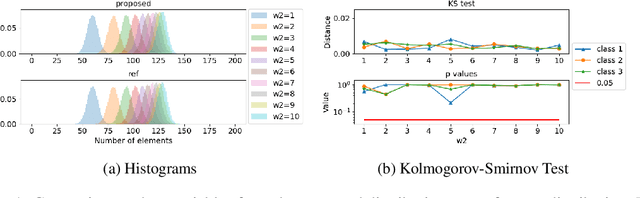
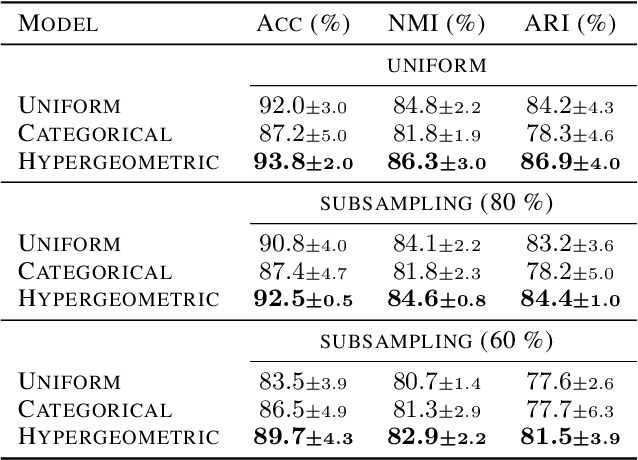
Partitioning a set of elements into a given number of groups of a priori unknown sizes is an important task in many applications. Due to hard constraints, it is a non-differentiable problem which prohibits its direct use in modern machine learning frameworks. Hence, previous works mostly fall back on suboptimal heuristics or simplified assumptions. The multivariate hypergeometric distribution offers a probabilistic formulation of how to distribute a given number of samples across multiple groups. Unfortunately, as a discrete probability distribution, it neither is differentiable. In this work, we propose a continuous relaxation for the multivariate non-central hypergeometric distribution. We introduce an efficient and numerically stable sampling procedure. This enables reparameterized gradients for the hypergeometric distribution and its integration into automatic differentiation frameworks. We highlight the applicability and usability of the proposed formulation on two different common machine learning tasks.

On the Limitations of Multimodal VAEs

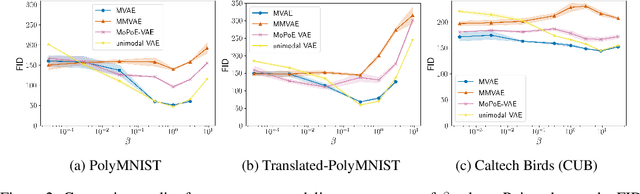
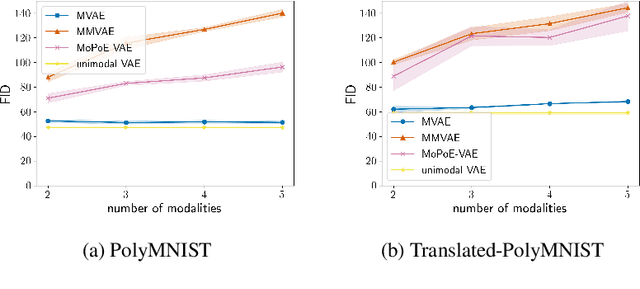
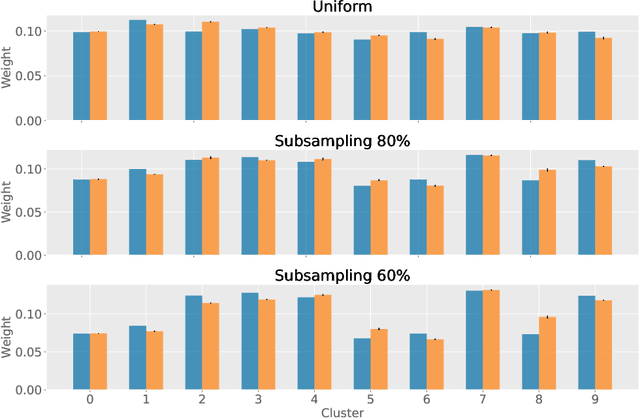
Multimodal variational autoencoders (VAEs) have shown promise as efficient generative models for weakly-supervised data. Yet, despite their advantage of weak supervision, they exhibit a gap in generative quality compared to unimodal VAEs, which are completely unsupervised. In an attempt to explain this gap, we uncover a fundamental limitation that applies to a large family of mixture-based multimodal VAEs. We prove that the sub-sampling of modalities enforces an undesirable upper bound on the multimodal ELBO and thereby limits the generative quality of the respective models. Empirically, we showcase the generative quality gap on both synthetic and real data and present the tradeoffs between different variants of multimodal VAEs. We find that none of the existing approaches fulfills all desired criteria of an effective multimodal generative model when applied on more complex datasets than those used in previous benchmarks. In summary, we identify, formalize, and validate fundamental limitations of VAE-based approaches for modeling weakly-supervised data and discuss implications for real-world applications.

Generalized Multimodal ELBO

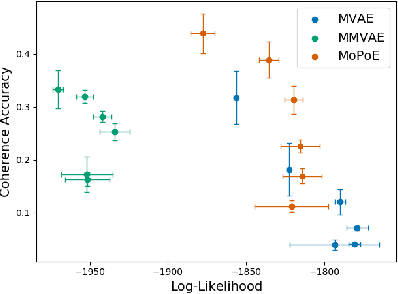
Multiple data types naturally co-occur when describing real-world phenomena and learning from them is a long-standing goal in machine learning research. However, existing self-supervised generative models approximating an ELBO are not able to fulfill all desired requirements of multimodal models: their posterior approximation functions lead to a trade-off between the semantic coherence and the ability to learn the joint data distribution. We propose a new, generalized ELBO formulation for multimodal data that overcomes these limitations. The new objective encompasses two previous methods as special cases and combines their benefits without compromises. In extensive experiments, we demonstrate the advantage of the proposed method compared to state-of-the-art models in self-supervised, generative learning tasks.

Multimodal Generative Learning Utilizing Jensen-Shannon-Divergence

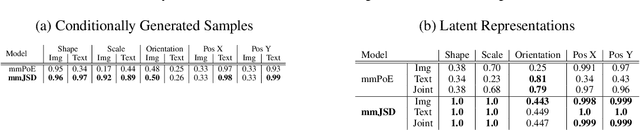
Learning from different data types is a long-standing goal in machine learning research, as multiple information sources co-occur when describing natural phenomena. However, existing generative models that approximate a multimodal ELBO rely on difficult or inefficient training schemes to learn a joint distribution and the dependencies between modalities. In this work, we propose a novel, efficient objective function that utilizes the Jensen-Shannon divergence for multiple distributions. It simultaneously approximates the unimodal and joint multimodal posteriors directly via a dynamic prior. In addition, we theoretically prove that the new multimodal JS-divergence (mmJSD) objective optimizes an ELBO. In extensive experiments, we demonstrate the advantage of the proposed mmJSD model compared to previous work in unsupervised, generative learning tasks.