Alexander Marx
Regression-Based Estimation of Causal Effects in the Presence of Selection Bias and Confounding
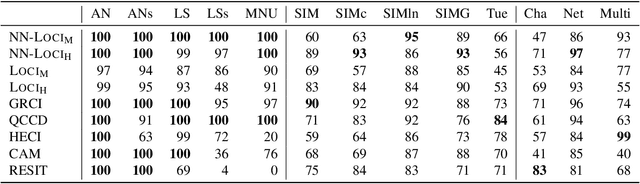
Mar 26, 2025Abstract:We consider the problem of estimating the expected causal effect $E[Y|do(X)]$ for a target variable $Y$ when treatment $X$ is set by intervention, focusing on continuous random variables. In settings without selection bias or confounding, $E[Y|do(X)] = E[Y|X]$, which can be estimated using standard regression methods. However, regression fails when systematic missingness induced by selection bias, or confounding distorts the data. Boeken et al. [2023] show that when training data is subject to selection, proxy variables unaffected by this process can, under certain constraints, be used to correct for selection bias to estimate $E[Y|X]$, and hence $E[Y|do(X)]$, reliably. When data is additionally affected by confounding, however, this equality is no longer valid. Building on these results, we consider a more general setting and propose a framework that incorporates both selection bias and confounding. Specifically, we derive theoretical conditions ensuring identifiability and recoverability of causal effects under access to external data and proxy variables. We further introduce a two-step regression estimator (TSR), capable of exploiting proxy variables to adjust for selection bias while accounting for confounding. We show that TSR coincides with prior work if confounding is absent, but achieves a lower variance. Extensive simulation studies validate TSR's correctness for scenarios which may include both selection bias and confounding with proxy variables.
A Cautionary Tale About "Neutrally" Informative AI Tools Ahead of the 2025 Federal Elections in Germany
Feb 21, 2025Abstract:In this study, we examine the reliability of AI-based Voting Advice Applications (VAAs) and large language models (LLMs) in providing objective political information. Our analysis is based upon a comparison with party responses to 38 statements of the Wahl-O-Mat, a well-established German online tool that helps inform voters by comparing their views with political party positions. For the LLMs, we identify significant biases. They exhibit a strong alignment (over 75% on average) with left-wing parties and a substantially lower alignment with center-right (smaller 50%) and right-wing parties (around 30%). Furthermore, for the VAAs, intended to objectively inform voters, we found substantial deviations from the parties' stated positions in Wahl-O-Mat: While one VAA deviated in 25% of cases, another VAA showed deviations in more than 50% of cases. For the latter, we even observed that simple prompt injections led to severe hallucinations, including false claims such as non-existent connections between political parties and right-wing extremist ties.
Anomaly Detection by Context Contrasting
May 29, 2024


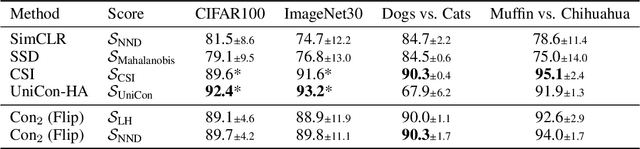
Abstract:Anomaly Detection focuses on identifying samples that deviate from the norm. When working with high-dimensional data such as images, a crucial requirement for detecting anomalous patterns is learning lower-dimensional representations that capture normal concepts seen during training. Recent advances in self-supervised learning have shown great promise in this regard. However, many of the most successful self-supervised anomaly detection methods assume prior knowledge about the structure of anomalies and leverage synthetic anomalies during training. Yet, in many real-world applications, we do not know what to expect from unseen data, and we can solely leverage knowledge about normal data. In this work, we propose Con2, which addresses this problem by setting normal training data into distinct contexts while preserving its normal properties, letting us observe the data from different perspectives. Unseen normal data consequently adheres to learned context representations while anomalies fail to do so, letting us detect them without any knowledge about anomalies during training. Our experiments demonstrate that our approach achieves state-of-the-art performance on various benchmarks while exhibiting superior performance in a more realistic healthcare setting, where knowledge about potential anomalies is often scarce.
The Mixtures and the Neural Critics: On the Pointwise Mutual Information Profiles of Fine Distributions
Oct 16, 2023
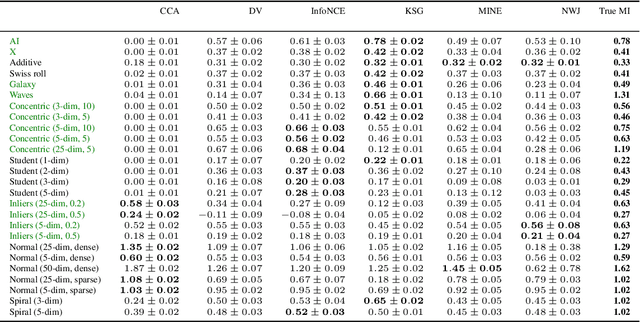

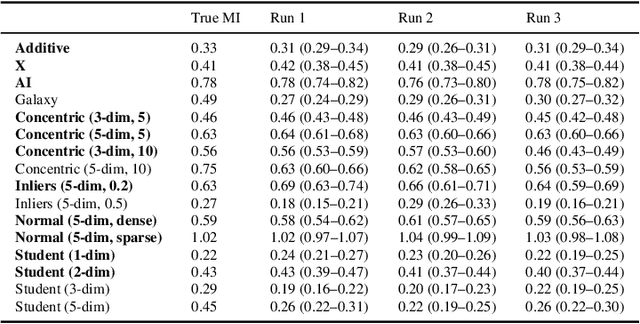
Abstract:Mutual information quantifies the dependence between two random variables and remains invariant under diffeomorphisms. In this paper, we explore the pointwise mutual information profile, an extension of mutual information that maintains this invariance. We analytically describe the profiles of multivariate normal distributions and introduce the family of fine distributions, for which the profile can be accurately approximated using Monte Carlo methods. We then show how fine distributions can be used to study the limitations of existing mutual information estimators, investigate the behavior of neural critics used in variational estimators, and understand the effect of experimental outliers on mutual information estimation. Finally, we show how fine distributions can be used to obtain model-based Bayesian estimates of mutual information, suitable for problems with available domain expertise in which uncertainty quantification is necessary.
Exploiting Causal Graph Priors with Posterior Sampling for Reinforcement Learning
Oct 11, 2023

Abstract:Posterior sampling allows the exploitation of prior knowledge of the environment's transition dynamics to improve the sample efficiency of reinforcement learning. The prior is typically specified as a class of parametric distributions, a task that can be cumbersome in practice, often resulting in the choice of uninformative priors. In this work, we propose a novel posterior sampling approach in which the prior is given as a (partial) causal graph over the environment's variables. The latter is often more natural to design, such as listing known causal dependencies between biometric features in a medical treatment study. Specifically, we propose a hierarchical Bayesian procedure, called C-PSRL, simultaneously learning the full causal graph at the higher level and the parameters of the resulting factored dynamics at the lower level. For this procedure, we provide an analysis of its Bayesian regret, which explicitly connects the regret rate with the degree of prior knowledge. Our numerical evaluation conducted in illustrative domains confirms that C-PSRL strongly improves the efficiency of posterior sampling with an uninformative prior while performing close to posterior sampling with the full causal graph.
Beyond Normal: On the Evaluation of Mutual Information Estimators
Jun 19, 2023

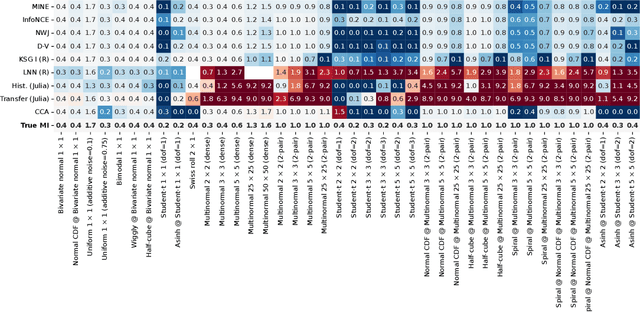
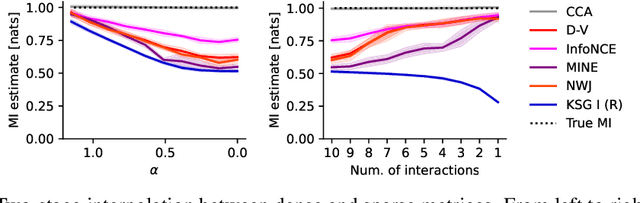
Abstract:Mutual information is a general statistical dependency measure which has found applications in representation learning, causality, domain generalization and computational biology. However, mutual information estimators are typically evaluated on simple families of probability distributions, namely multivariate normal distribution and selected distributions with one-dimensional random variables. In this paper, we show how to construct a diverse family of distributions with known ground-truth mutual information and propose a language-independent benchmarking platform for mutual information estimators. We discuss the general applicability and limitations of classical and neural estimators in settings involving high dimensions, sparse interactions, long-tailed distributions, and high mutual information. Finally, we provide guidelines for practitioners on how to select appropriate estimator adapted to the difficulty of problem considered and issues one needs to consider when applying an estimator to a new data set.
Identifiability Results for Multimodal Contrastive Learning
Mar 16, 2023



Abstract:Contrastive learning is a cornerstone underlying recent progress in multi-view and multimodal learning, e.g., in representation learning with image/caption pairs. While its effectiveness is not yet fully understood, a line of recent work reveals that contrastive learning can invert the data generating process and recover ground truth latent factors shared between views. In this work, we present new identifiability results for multimodal contrastive learning, showing that it is possible to recover shared factors in a more general setup than the multi-view setting studied previously. Specifically, we distinguish between the multi-view setting with one generative mechanism (e.g., multiple cameras of the same type) and the multimodal setting that is characterized by distinct mechanisms (e.g., cameras and microphones). Our work generalizes previous identifiability results by redefining the generative process in terms of distinct mechanisms with modality-specific latent variables. We prove that contrastive learning can block-identify latent factors shared between modalities, even when there are nontrivial dependencies between factors. We empirically verify our identifiability results with numerical simulations and corroborate our findings on a complex multimodal dataset of image/text pairs. Zooming out, our work provides a theoretical basis for multimodal representation learning and explains in which settings multimodal contrastive learning can be effective in practice.
On the Identifiability and Estimation of Causal Location-Scale Noise Models
Oct 13, 2022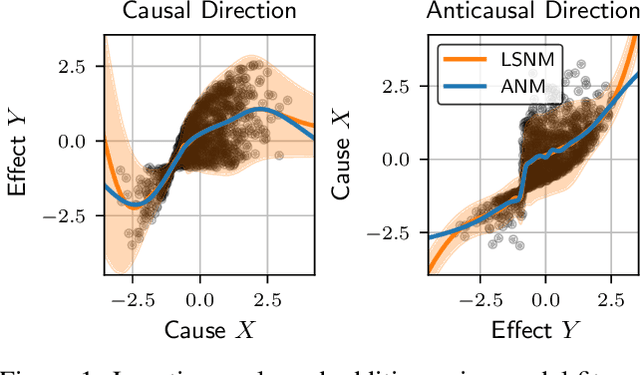
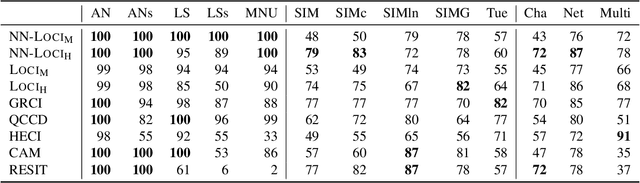
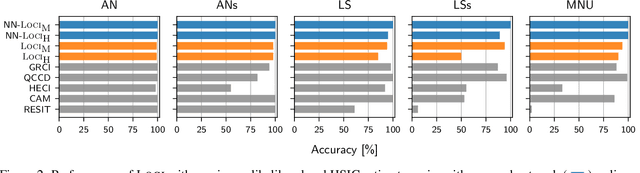
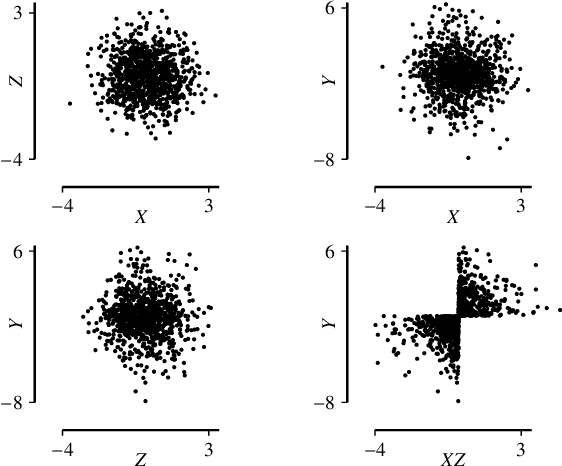
Abstract:We study the class of location-scale or heteroscedastic noise models (LSNMs), in which the effect $Y$ can be written as a function of the cause $X$ and a noise source $N$ independent of $X$, which may be scaled by a positive function $g$ over the cause, i.e., $Y = f(X) + g(X)N$. Despite the generality of the model class, we show the causal direction is identifiable up to some pathological cases. To empirically validate these theoretical findings, we propose two estimators for LSNMs: an estimator based on (non-linear) feature maps, and one based on probabilistic neural networks. Both model the conditional distribution of $Y$ given $X$ as a Gaussian parameterized by its natural parameters. Since the neural network approach can fit functions of arbitrary complexity, it has an edge over the feature map-based approach in terms of empirical performance. When the feature maps are correctly specified, however, we can prove that our estimator is jointly concave, which allows us to derive stronger guarantees for the cause-effect identification task.
A Weaker Faithfulness Assumption based on Triple Interactions
Oct 27, 2020

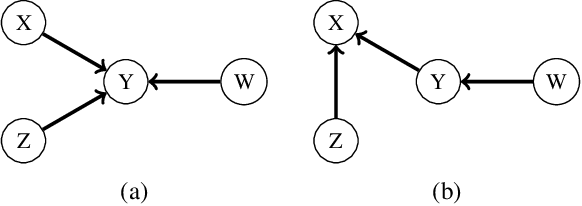
Abstract:One of the core assumptions in causal discovery is the faithfulness assumption---i.e. assuming that independencies found in the data are due to separations in the true causal graph. This assumption can, however, be violated in many ways, including xor connections, deterministic functions or cancelling paths. In this work, we propose a weaker assumption that we call 2-adjacency faithfulness. In contrast to adjacency faithfulness, which assumes that there is no conditional independence between each pair of variables that are connected in the causal graph, we only require no conditional independence between a node and a subset of its Markov blanket that can contain up to two nodes. Equivalently, we adapt orientation faithfulness to this setting. We further propose a sound orientation rule for causal discovery that applies under weaker assumptions. As a proof of concept, we derive a modified Grow and Shrink algorithm that recovers the Markov blanket of a target node and prove its correctness under strictly weaker assumptions than the standard faithfulness assumption.
Testing Conditional Independence on Discrete Data using Stochastic Complexity
Mar 12, 2019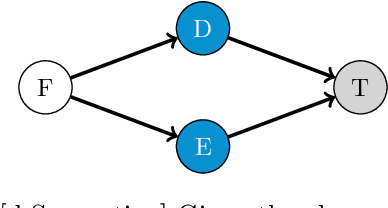
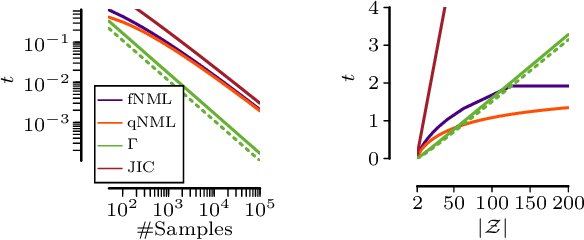
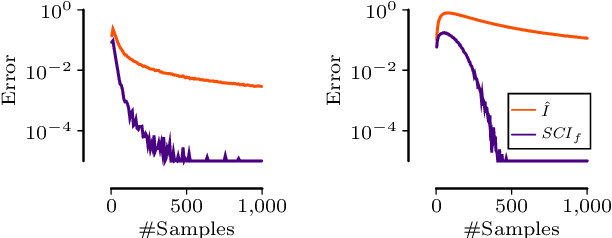
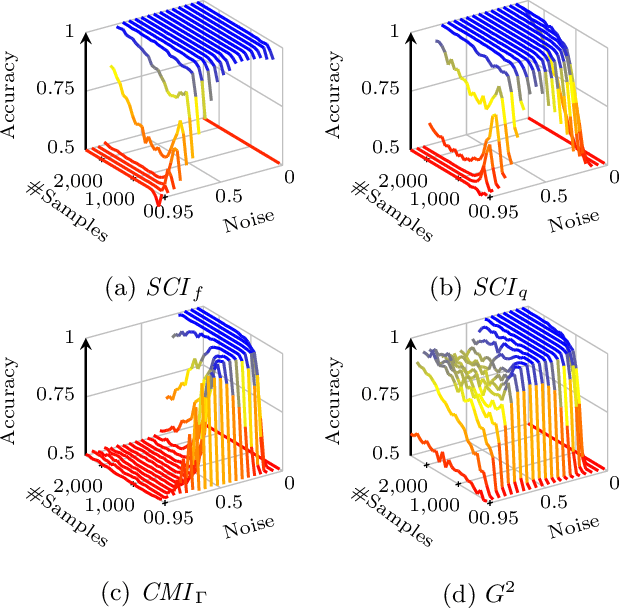
Abstract:Testing for conditional independence is a core aspect of constraint-based causal discovery. Although commonly used tests are perfect in theory, they often fail to reject independence in practice, especially when conditioning on multiple variables. We focus on discrete data and propose a new test based on the notion of algorithmic independence that we instantiate using stochastic complexity. Amongst others, we show that our proposed test, SCI, is an asymptotically unbiased as well as $L_2$ consistent estimator for conditional mutual information (CMI). Further, we show that SCI can be reformulated to find a sensible threshold for CMI that works well on limited samples. Empirical evaluation shows that SCI has a lower type II error than commonly used tests. As a result, we obtain a higher recall when we use SCI in causal discovery algorithms, without compromising the precision.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge