Fair Clustering: A Causal Perspective

Clustering algorithms may unintentionally propagate or intensify existing disparities, leading to unfair representations or biased decision-making. Current fair clustering methods rely on notions of fairness that do not capture any information on the underlying causal mechanisms. We show that optimising for non-causal fairness notions can paradoxically induce direct discriminatory effects from a causal standpoint. We present a clustering approach that incorporates causal fairness metrics to provide a more nuanced approach to fairness in unsupervised learning. Our approach enables the specification of the causal fairness metrics that should be minimised. We demonstrate the efficacy of our methodology using datasets known to harbour unfair biases.

The Mixtures and the Neural Critics: On the Pointwise Mutual Information Profiles of Fine Distributions

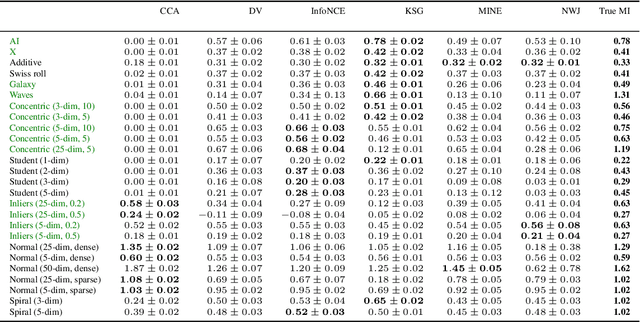
Mutual information quantifies the dependence between two random variables and remains invariant under diffeomorphisms. In this paper, we explore the pointwise mutual information profile, an extension of mutual information that maintains this invariance. We analytically describe the profiles of multivariate normal distributions and introduce the family of fine distributions, for which the profile can be accurately approximated using Monte Carlo methods. We then show how fine distributions can be used to study the limitations of existing mutual information estimators, investigate the behavior of neural critics used in variational estimators, and understand the effect of experimental outliers on mutual information estimation. Finally, we show how fine distributions can be used to obtain model-based Bayesian estimates of mutual information, suitable for problems with available domain expertise in which uncertainty quantification is necessary.

Beyond Normal: On the Evaluation of Mutual Information Estimators

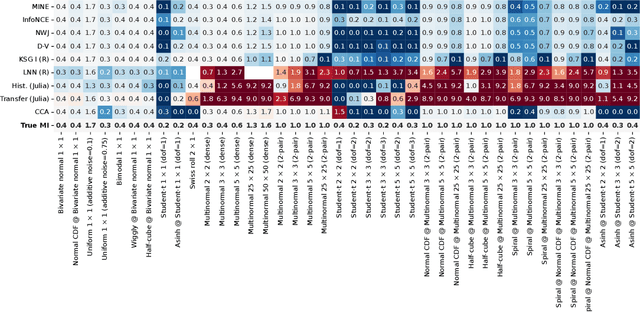
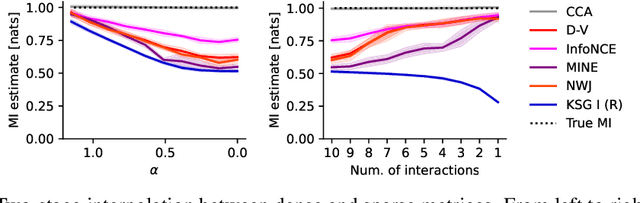
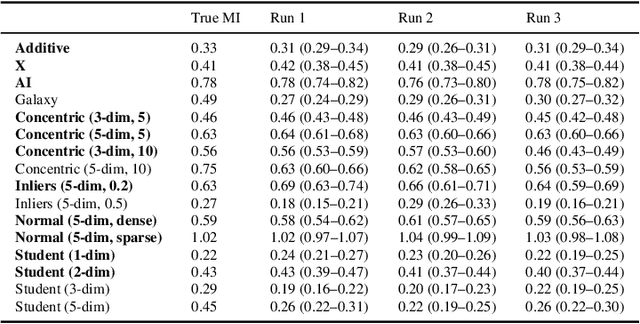
Mutual information is a general statistical dependency measure which has found applications in representation learning, causality, domain generalization and computational biology. However, mutual information estimators are typically evaluated on simple families of probability distributions, namely multivariate normal distribution and selected distributions with one-dimensional random variables. In this paper, we show how to construct a diverse family of distributions with known ground-truth mutual information and propose a language-independent benchmarking platform for mutual information estimators. We discuss the general applicability and limitations of classical and neural estimators in settings involving high dimensions, sparse interactions, long-tailed distributions, and high mutual information. Finally, we provide guidelines for practitioners on how to select appropriate estimator adapted to the difficulty of problem considered and issues one needs to consider when applying an estimator to a new data set.

Marginalization in Bayesian Networks: Integrating Exact and Approximate Inference

Bayesian Networks are probabilistic graphical models that can compactly represent dependencies among random variables. Missing data and hidden variables require calculating the marginal probability distribution of a subset of the variables. While knowledge of the marginal probability distribution is crucial for various problems in statistics and machine learning, its exact computation is generally not feasible for categorical variables due to the NP-hardness of this task. We develop a divide-and-conquer approach using the graphical properties of Bayesian networks to split the computation of the marginal probability distribution into sub-calculations of lower dimensionality, reducing the overall computational complexity. Exploiting this property, we present an efficient and scalable algorithm for estimating the marginal probability distribution for categorical variables. The novel method is compared against state-of-the-art approximate inference methods in a benchmarking study, where it displays superior performance. As an immediate application, we demonstrate how the marginal probability distribution can be used to classify incomplete data against Bayesian networks and use this approach for identifying the cancer subtype of kidney cancer patient samples.

Bayesian structure learning and sampling of Bayesian networks with the R package BiDAG

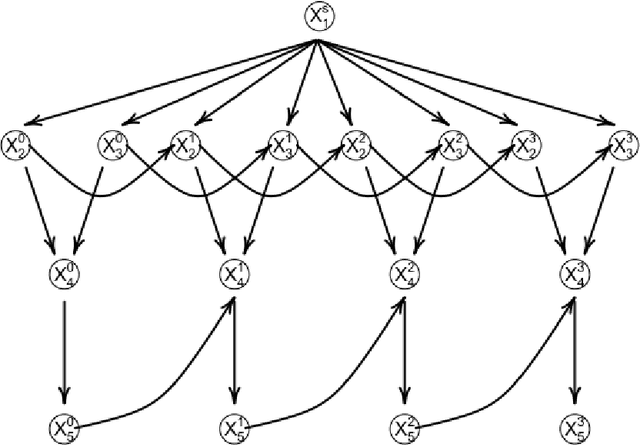
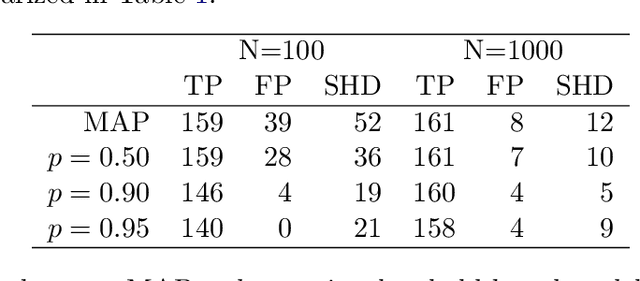
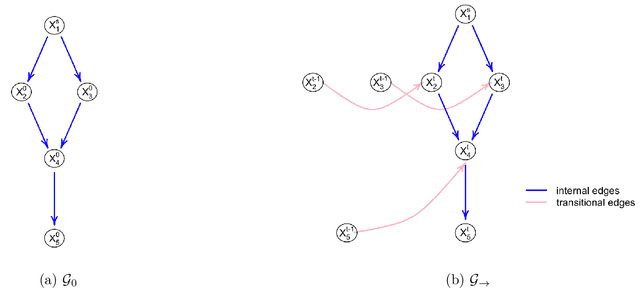
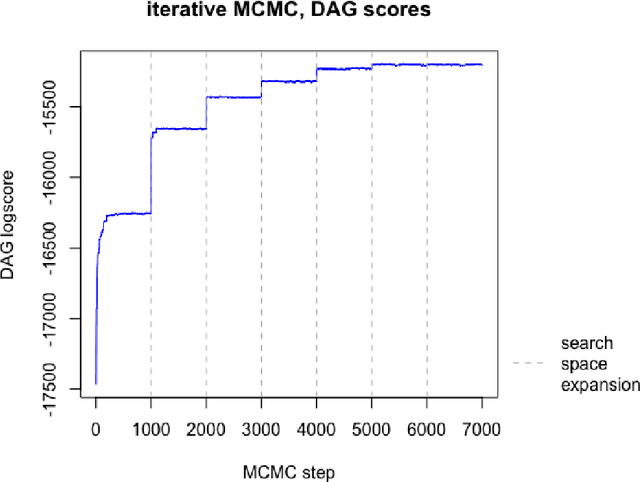
The R package BiDAG implements Markov chain Monte Carlo (MCMC) methods for structure learning and sampling of Bayesian networks. The package includes tools to search for a maximum a posteriori (MAP) graph and to sample graphs from the posterior distribution given the data. A new hybrid approach to structure learning enables inference in large graphs. In the first step, we define a reduced search space by means of the PC algorithm or based on prior knowledge. In the second step, an iterative order MCMC scheme proceeds to optimize within the restricted search space and estimate the MAP graph. Sampling from the posterior distribution is implemented using either order or partition MCMC. The models and algorithms can handle both discrete and continuous data. The BiDAG package also provides an implementation of MCMC schemes for structure learning and sampling of dynamic Bayesian networks.