The Mixtures and the Neural Critics: On the Pointwise Mutual Information Profiles of Fine Distributions

Mutual information quantifies the dependence between two random variables and remains invariant under diffeomorphisms. In this paper, we explore the pointwise mutual information profile, an extension of mutual information that maintains this invariance. We analytically describe the profiles of multivariate normal distributions and introduce the family of fine distributions, for which the profile can be accurately approximated using Monte Carlo methods. We then show how fine distributions can be used to study the limitations of existing mutual information estimators, investigate the behavior of neural critics used in variational estimators, and understand the effect of experimental outliers on mutual information estimation. Finally, we show how fine distributions can be used to obtain model-based Bayesian estimates of mutual information, suitable for problems with available domain expertise in which uncertainty quantification is necessary.

Beyond Normal: On the Evaluation of Mutual Information Estimators

Mutual information is a general statistical dependency measure which has found applications in representation learning, causality, domain generalization and computational biology. However, mutual information estimators are typically evaluated on simple families of probability distributions, namely multivariate normal distribution and selected distributions with one-dimensional random variables. In this paper, we show how to construct a diverse family of distributions with known ground-truth mutual information and propose a language-independent benchmarking platform for mutual information estimators. We discuss the general applicability and limitations of classical and neural estimators in settings involving high dimensions, sparse interactions, long-tailed distributions, and high mutual information. Finally, we provide guidelines for practitioners on how to select appropriate estimator adapted to the difficulty of problem considered and issues one needs to consider when applying an estimator to a new data set.

Bayesian Quantification with Black-Box Estimators

Understanding how different classes are distributed in an unlabeled data set is an important challenge for the calibration of probabilistic classifiers and uncertainty quantification. Approaches like adjusted classify and count, black-box shift estimators, and invariant ratio estimators use an auxiliary (and potentially biased) black-box classifier trained on a different (shifted) data set to estimate the class distribution and yield asymptotic guarantees under weak assumptions. We demonstrate that all these algorithms are closely related to the inference in a particular Bayesian model, approximating the assumed ground-truth generative process. Then, we discuss an efficient Markov Chain Monte Carlo sampling scheme for the introduced model and show an asymptotic consistency guarantee in the large-data limit. We compare the introduced model against the established point estimators in a variety of scenarios, and show it is competitive, and in some cases superior, with the state of the art.

Unsupervised Recalibration

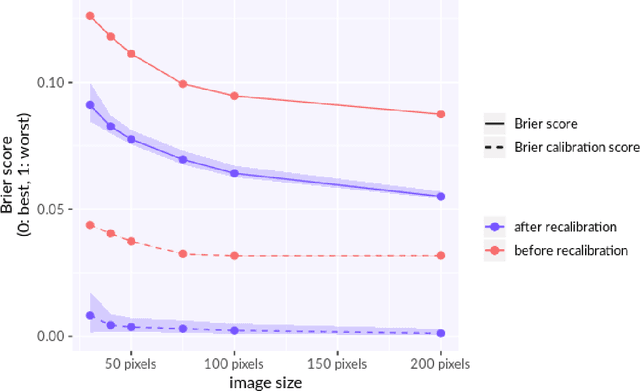
Unsupervised recalibration (URC) is a general way to improve the accuracy of an already trained probabilistic classification or regression model upon encountering new data while deployed in the field. URC does not require any ground truth associated with the new field data. URC merely observes the model's predictions and recognizes when the training set is not representative of field data, and then corrects to remove any introduced bias. URC can be particularly useful when applied separately to different subpopulations observed in the field that were not considered as features when training the machine learning model. This makes it possible to exploit subpopulation information without retraining the model or even having ground truth for some or all subpopulations available. Additionally, if these subpopulations are the object of study, URC serves to determine the correct ground truth distributions for them, where naive aggregation methods, like averaging the model's predictions, systematically underestimate their differences.