Bolek: A Multimodal Language Model for Molecular Reasoning

Molecular property models increasingly support high-stakes drug-discovery decisions, but their outputs are often difficult to audit: classical predictors return scores without rationale, while language models can produce fluent explanations weakly grounded in the input molecule. We introduce Bolek, a compact multimodal language model that grounds natural-language reasoning in molecular structure by injecting a Morgan fingerprint embedding into an instruction-tuned text decoder. Bolek is fine-tuned on molecular alignment tasks, including molecule description, RDKit descriptor prediction, and substructure detection, and on downstream reasoning over 15 TDC binary classification tasks using synthetic chains-of-thought anchored in concrete molecular features. Across these tasks, Bolek outperforms its Qwen3-4B-Instruct base on all endpoints in yes/no mode and on 13 of 15 in chain-of-thought mode, raising mean ROC/PR AUC from 0.55 to 0.76. It also outperforms TxGemma-9B-Chat on 13 of 15 binary classification tasks despite being less than half its size. Bolek's explanations are more grounded than those of the baseline LLMs: it cites numerical descriptors 10-100x more often per chain-of-thought, and the cited values agree strongly with RDKit for key descriptors such as TPSA, MolLogP, and MolWt (Spearman rho = 0.87-0.91). Generalisation extends beyond the training panel: on 15 unseen TDC classification endpoints, Bolek matches TxGemma on five, and it produces non-trivial rank correlations on three held-out regression endpoints despite never seeing downstream regression during training. These results suggest that targeted modality injection and reasoning supervision tied to verifiable molecular features can yield compact, auditable molecular reasoning models.

The Mixtures and the Neural Critics: On the Pointwise Mutual Information Profiles of Fine Distributions

Mutual information quantifies the dependence between two random variables and remains invariant under diffeomorphisms. In this paper, we explore the pointwise mutual information profile, an extension of mutual information that maintains this invariance. We analytically describe the profiles of multivariate normal distributions and introduce the family of fine distributions, for which the profile can be accurately approximated using Monte Carlo methods. We then show how fine distributions can be used to study the limitations of existing mutual information estimators, investigate the behavior of neural critics used in variational estimators, and understand the effect of experimental outliers on mutual information estimation. Finally, we show how fine distributions can be used to obtain model-based Bayesian estimates of mutual information, suitable for problems with available domain expertise in which uncertainty quantification is necessary.

Beyond Normal: On the Evaluation of Mutual Information Estimators

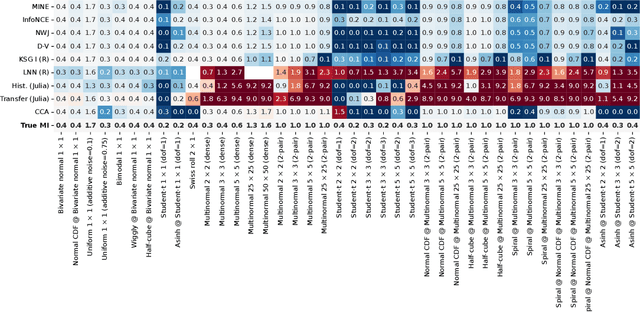
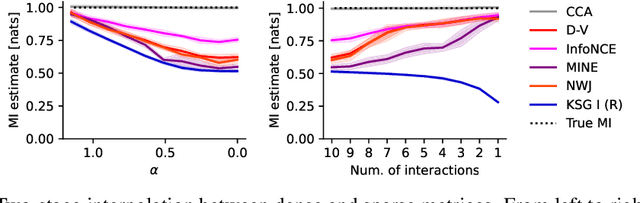
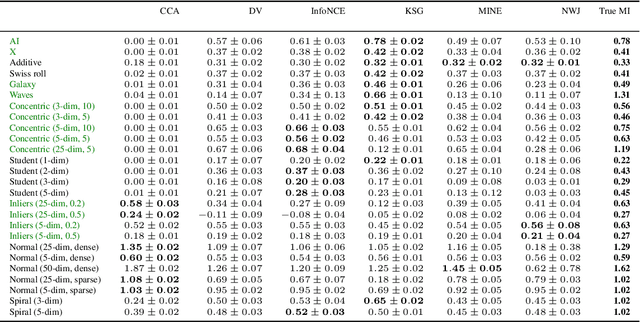
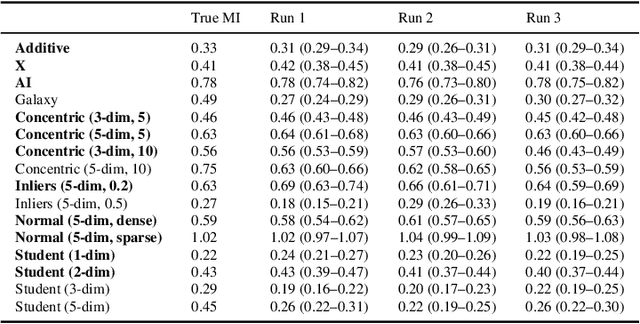
Mutual information is a general statistical dependency measure which has found applications in representation learning, causality, domain generalization and computational biology. However, mutual information estimators are typically evaluated on simple families of probability distributions, namely multivariate normal distribution and selected distributions with one-dimensional random variables. In this paper, we show how to construct a diverse family of distributions with known ground-truth mutual information and propose a language-independent benchmarking platform for mutual information estimators. We discuss the general applicability and limitations of classical and neural estimators in settings involving high dimensions, sparse interactions, long-tailed distributions, and high mutual information. Finally, we provide guidelines for practitioners on how to select appropriate estimator adapted to the difficulty of problem considered and issues one needs to consider when applying an estimator to a new data set.