Exact discovery is polynomial for sparse causal Bayesian networks

Causal Bayesian networks are widely used tools for summarising the dependencies between variables and elucidating their putative causal relationships. Learning networks from data is computationally hard in general. The current state-of-the-art approaches for exact causal discovery are integer linear programming over the underlying space of directed acyclic graphs, dynamic programming and shortest-path searches over the space of topological orders, and constraint programming combining both. For dynamic programming over orders, the computational complexity is known to be exponential base 2 in the number of variables in the network. We demonstrate how to use properties of Bayesian networks to prune the search space and lower the computational cost, while still guaranteeing exact discovery. When including new path-search and divide-and-conquer criteria, we prove optimality in quadratic time for matchings, and polynomial time for any network class with logarithmically-bound largest connected components. In simulation studies we observe the polynomial dependence for sparse networks and that, beyond some critical value, the logarithm of the base grows with the network density. Our approach then out-competes the state-of-the-art at lower densities. These results therefore pave the way for faster exact causal discovery in larger and sparser networks.

Bayesian Causal Inference with Gaussian Process Networks

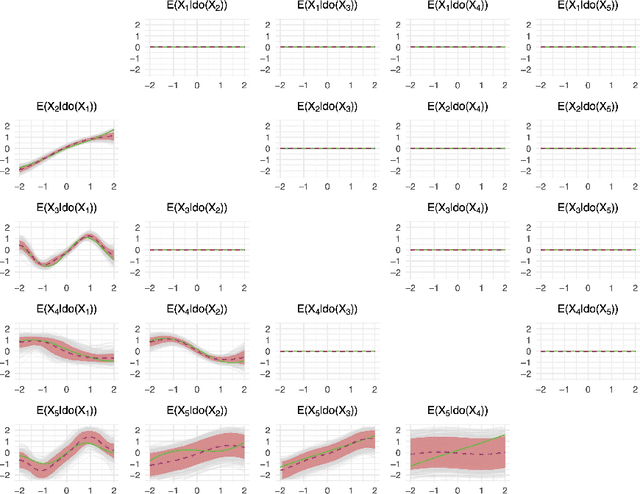
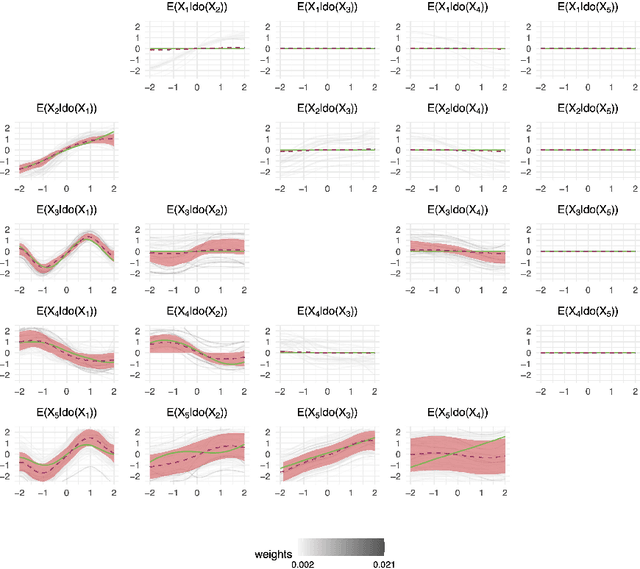
Causal discovery and inference from observational data is an essential problem in statistics posing both modeling and computational challenges. These are typically addressed by imposing strict assumptions on the joint distribution such as linearity. We consider the problem of the Bayesian estimation of the effects of hypothetical interventions in the Gaussian Process Network (GPN) model, a flexible causal framework which allows describing the causal relationships nonparametrically. We detail how to perform causal inference on GPNs by simulating the effect of an intervention across the whole network and propagating the effect of the intervention on downstream variables. We further derive a simpler computational approximation by estimating the intervention distribution as a function of local variables only, modeling the conditional distributions via additive Gaussian processes. We extend both frameworks beyond the case of a known causal graph, incorporating uncertainty about the causal structure via Markov chain Monte Carlo methods. Simulation studies show that our approach is able to identify the effects of hypothetical interventions with non-Gaussian, non-linear observational data and accurately reflect the posterior uncertainty of the causal estimates. Finally we compare the results of our GPN-based causal inference approach to existing methods on a dataset of $A.~thaliana$ gene expressions.

A Bayesian Take on Gaussian Process Networks

Gaussian Process Networks (GPNs) are a class of directed graphical models which employ Gaussian processes as priors for the conditional expectation of each variable given its parents in the network. The model allows describing continuous joint distributions in a compact but flexible manner with minimal parametric assumptions on the dependencies between variables. Bayesian structure learning of GPNs requires computing the posterior over graphs of the network and is computationally infeasible even in low dimensions. This work implements Monte Carlo and Markov Chain Monte Carlo methods to sample from the posterior distribution of network structures. As such, the approach follows the Bayesian paradigm, comparing models via their marginal likelihood and computing the posterior probability of the GPN features. Simulation studies show that our method outperforms state-of-the-art algorithms in recovering the graphical structure of the network and provides an accurate approximation of its posterior distribution.

The interventional Bayesian Gaussian equivalent score for Bayesian causal inference with unknown soft interventions

Describing the causal relations governing a system is a fundamental task in many scientific fields, ideally addressed by experimental studies. However, obtaining data under intervention scenarios may not always be feasible, while discovering causal relations from purely observational data is notoriously challenging. In certain settings, such as genomics, we may have data from heterogeneous study conditions, with soft (partial) interventions only pertaining to a subset of the study variables, whose effects and targets are possibly unknown. Combining data from experimental and observational studies offers the opportunity to leverage both domains and improve on the identifiability of causal structures. To this end, we define the interventional BGe score for a mixture of observational and interventional data, where the targets and effects of intervention may be unknown. To demonstrate the approach we compare its performance to other state-of-the-art algorithms, both in simulations and data analysis applications. Prerogative of our method is that it takes a Bayesian perspective leading to a full characterisation of the posterior distribution of the DAG structures. Given a sample of DAGs one can also automatically derive full posterior distributions of the intervention effects. Consequently the method effectively captures the uncertainty both in the structure and the parameter estimates. Codes to reproduce the simulations and analyses are publicly available at github.com/jackkuipers/iBGe

Marginalization in Bayesian Networks: Integrating Exact and Approximate Inference

Bayesian Networks are probabilistic graphical models that can compactly represent dependencies among random variables. Missing data and hidden variables require calculating the marginal probability distribution of a subset of the variables. While knowledge of the marginal probability distribution is crucial for various problems in statistics and machine learning, its exact computation is generally not feasible for categorical variables due to the NP-hardness of this task. We develop a divide-and-conquer approach using the graphical properties of Bayesian networks to split the computation of the marginal probability distribution into sub-calculations of lower dimensionality, reducing the overall computational complexity. Exploiting this property, we present an efficient and scalable algorithm for estimating the marginal probability distribution for categorical variables. The novel method is compared against state-of-the-art approximate inference methods in a benchmarking study, where it displays superior performance. As an immediate application, we demonstrate how the marginal probability distribution can be used to classify incomplete data against Bayesian networks and use this approach for identifying the cancer subtype of kidney cancer patient samples.

The Dual PC Algorithm for Structure Learning

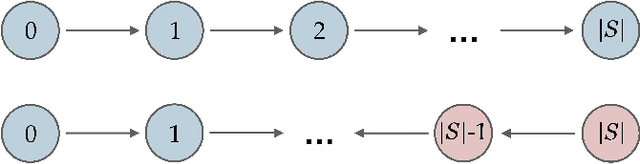
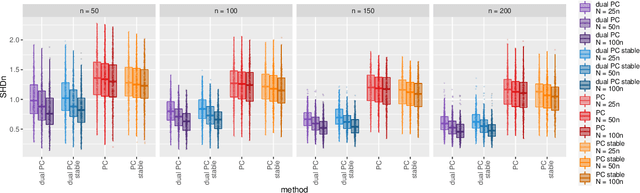
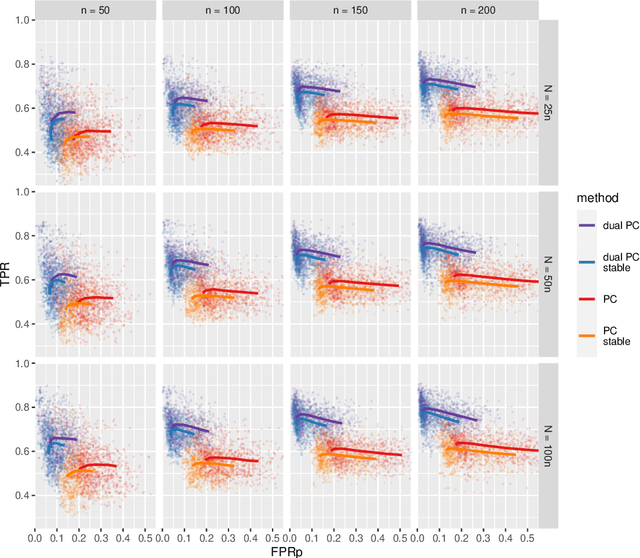
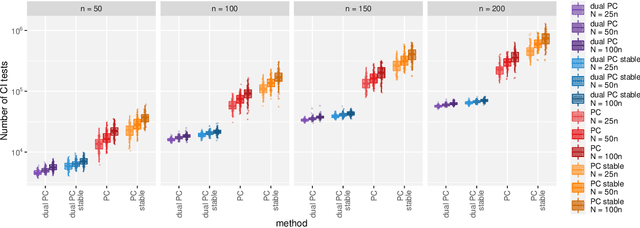
While learning the graphical structure of Bayesian networks from observational data is key to describing and helping understand data generating processes in complex applications, the task poses considerable challenges due to its computational complexity. The directed acyclic graph (DAG) representing a Bayesian network model is generally not identifiable from observational data, and a variety of methods exist to estimate its equivalence class instead. Under certain assumptions, the popular PC algorithm can consistently recover the correct equivalence class by testing for conditional independence (CI), starting from marginal independence relationships and progressively expanding the conditioning set. Here, we propose the dual PC algorithm, a novel scheme to carry out the CI tests within the PC algorithm by leveraging the inverse relationship between covariance and precision matrices. Notably, the elements of the precision matrix coincide with partial correlations for Gaussian data. Our algorithm then exploits block matrix inversions on the covariance and precision matrices to simultaneously perform tests on partial correlations of complementary (or dual) conditioning sets. The multiple CI tests of the dual PC algorithm, therefore, proceed by first considering marginal and full-order CI relationships and progressively moving to central-order ones. Simulation studies indicate that the dual PC algorithm outperforms the classical PC algorithm both in terms of run time and in recovering the underlying network structure.

Benchpress: a scalable and platform-independent workflow for benchmarking structure learning algorithms for graphical models

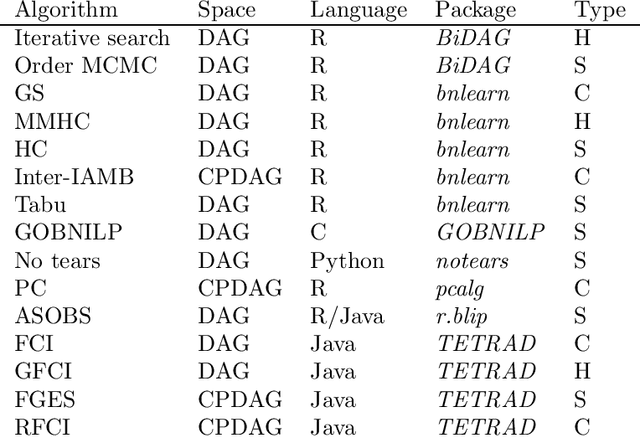
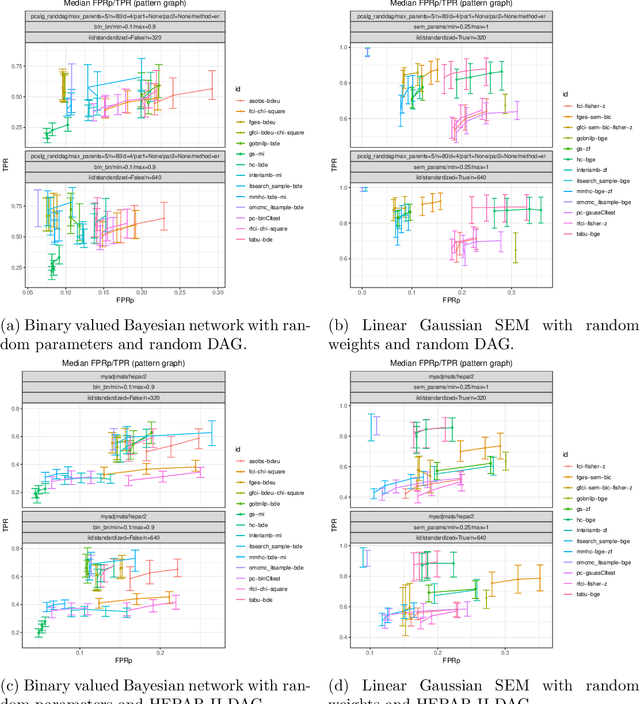
Describing the relationship between the variables in a study domain and modelling the data generating mechanism is a fundamental problem in many empirical sciences. Probabilistic graphical models are one common approach to tackle the problem. Learning the graphical structure is computationally challenging and a fervent area of current research with a plethora of algorithms being developed. To facilitate the benchmarking of different methods, we present a novel automated workflow, called benchpress for producing scalable, reproducible, and platform-independent benchmarks of structure learning algorithms for probabilistic graphical models. Benchpress is interfaced via a simple JSON-file, which makes it accessible for all users, while the code is designed in a fully modular fashion to enable researchers to contribute additional methodologies. Benchpress currently provides an interface to a large number of state-of-the-art algorithms from libraries such as BiDAG, bnlearn, GOBNILP, pcalg, r.blip, scikit-learn, TETRAD, and trilearn as well as a variety of methods for data generating models and performance evaluation. Alongside user-defined models and randomly generated datasets, the software tool also includes a number of standard datasets and graphical models from the literature, which may be included in a benchmarking workflow. We demonstrate the applicability of this workflow for learning Bayesian networks in four typical data scenarios. The source code and documentation is publicly available from http://github.com/felixleopoldo/benchpress.

Bayesian structure learning and sampling of Bayesian networks with the R package BiDAG

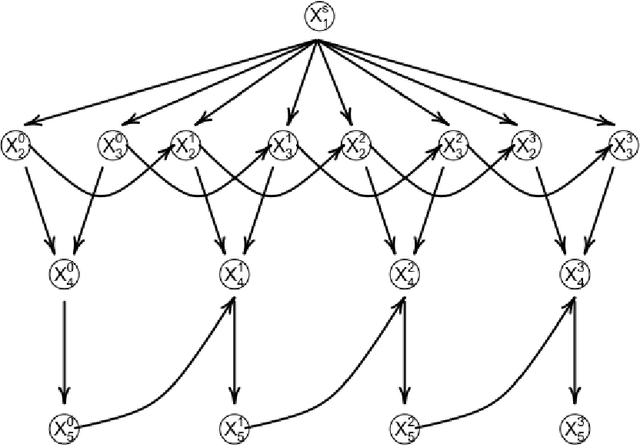
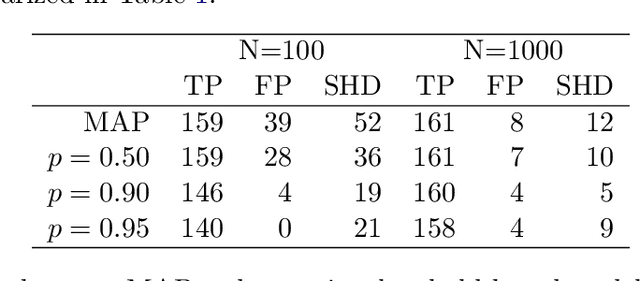
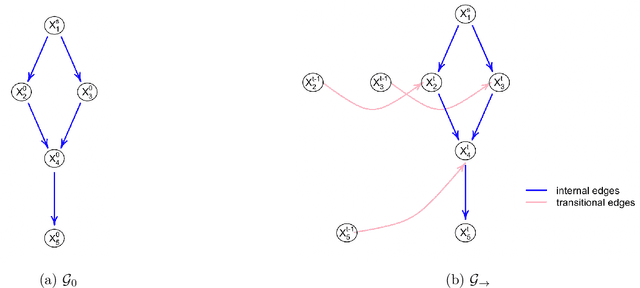
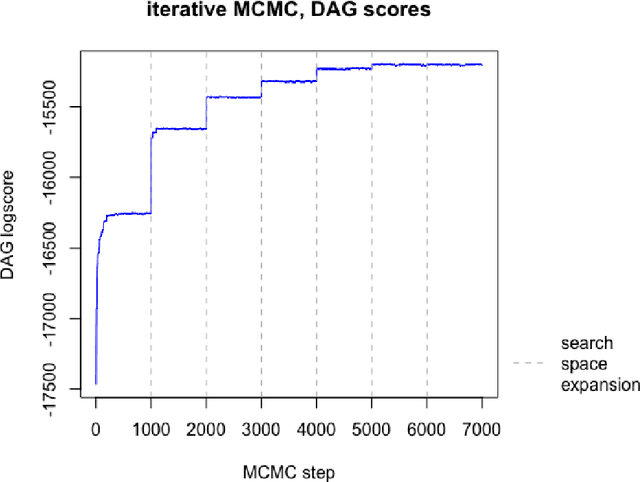
The R package BiDAG implements Markov chain Monte Carlo (MCMC) methods for structure learning and sampling of Bayesian networks. The package includes tools to search for a maximum a posteriori (MAP) graph and to sample graphs from the posterior distribution given the data. A new hybrid approach to structure learning enables inference in large graphs. In the first step, we define a reduced search space by means of the PC algorithm or based on prior knowledge. In the second step, an iterative order MCMC scheme proceeds to optimize within the restricted search space and estimate the MAP graph. Sampling from the posterior distribution is implemented using either order or partition MCMC. The models and algorithms can handle both discrete and continuous data. The BiDAG package also provides an implementation of MCMC schemes for structure learning and sampling of dynamic Bayesian networks.

Efficient Structure Learning and Sampling of Bayesian Networks

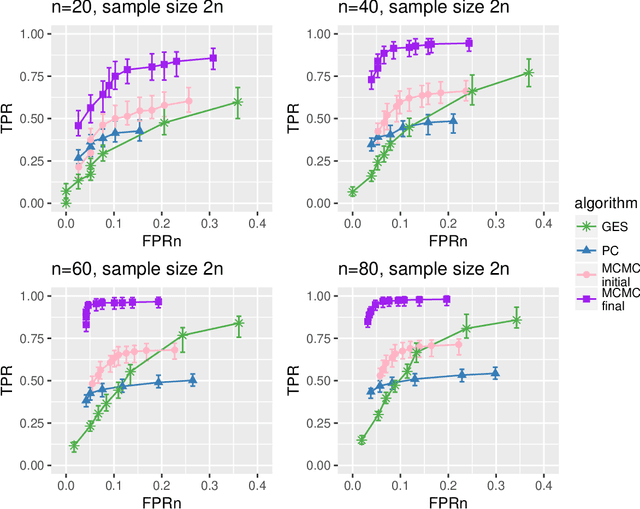
Bayesian networks are probabilistic graphical models widely employed to understand dependencies in high dimensional data, and even to facilitate causal discovery. Learning the underlying network structure, which is encoded as a directed acyclic graph (DAG) is highly challenging mainly due to the vast number of possible networks. Efforts have focussed on two fronts: constraint based methods that perform conditional independence tests to exclude edges and score and search approaches which explore the DAG space with greedy or MCMC schemes. Here we synthesise these two fields in a novel hybrid method which reduces the complexity of MCMC approaches to that of a constraint based method. Individual steps in the MCMC scheme only require simple table lookups so that very long chains can be efficiently obtained. Furthermore, the scheme includes an iterative procedure to correct for errors from the conditional independence tests. The algorithm not only offers markedly superior performance to alternatives, but DAGs can also be sampled from the posterior distribution enabling full Bayesian modelling averaging for much larger Bayesian networks.

Partition MCMC for inference on acyclic digraphs

Acyclic digraphs are the underlying representation of Bayesian networks, a widely used class of probabilistic graphical models. Learning the underlying graph from data is a way of gaining insights about the structural properties of a domain. Structure learning forms one of the inference challenges of statistical graphical models. MCMC methods, notably structure MCMC, to sample graphs from the posterior distribution given the data are probably the only viable option for Bayesian model averaging. Score modularity and restrictions on the number of parents of each node allow the graphs to be grouped into larger collections, which can be scored as a whole to improve the chain's convergence. Current examples of algorithms taking advantage of grouping are the biased order MCMC, which acts on the alternative space of permuted triangular matrices, and non ergodic edge reversal moves. Here we propose a novel algorithm, which employs the underlying combinatorial structure of DAGs to define a new grouping. As a result convergence is improved compared to structure MCMC, while still retaining the property of producing an unbiased sample. Finally the method can be combined with edge reversal moves to improve the sampler further.