The Dual PC Algorithm for Structure Learning
Paper and Code
Dec 16, 2021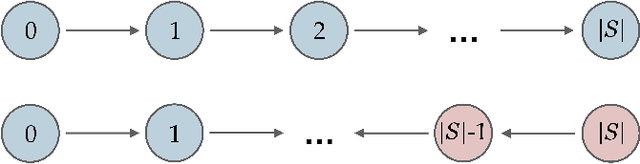
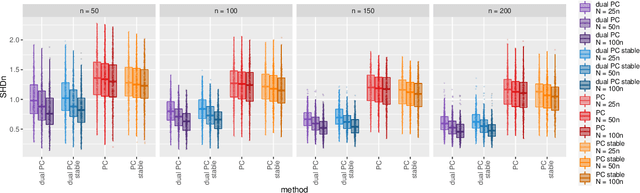
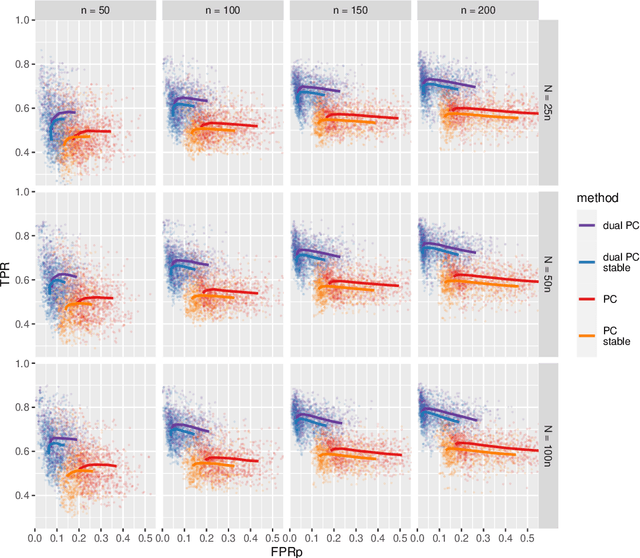
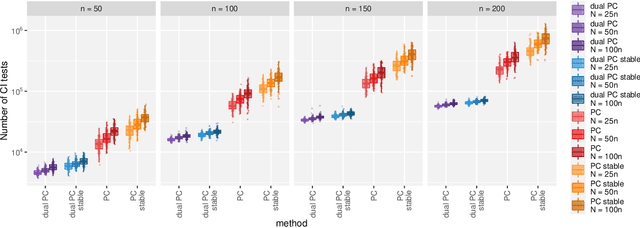
While learning the graphical structure of Bayesian networks from observational data is key to describing and helping understand data generating processes in complex applications, the task poses considerable challenges due to its computational complexity. The directed acyclic graph (DAG) representing a Bayesian network model is generally not identifiable from observational data, and a variety of methods exist to estimate its equivalence class instead. Under certain assumptions, the popular PC algorithm can consistently recover the correct equivalence class by testing for conditional independence (CI), starting from marginal independence relationships and progressively expanding the conditioning set. Here, we propose the dual PC algorithm, a novel scheme to carry out the CI tests within the PC algorithm by leveraging the inverse relationship between covariance and precision matrices. Notably, the elements of the precision matrix coincide with partial correlations for Gaussian data. Our algorithm then exploits block matrix inversions on the covariance and precision matrices to simultaneously perform tests on partial correlations of complementary (or dual) conditioning sets. The multiple CI tests of the dual PC algorithm, therefore, proceed by first considering marginal and full-order CI relationships and progressively moving to central-order ones. Simulation studies indicate that the dual PC algorithm outperforms the classical PC algorithm both in terms of run time and in recovering the underlying network structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge