Efficient Structure Learning and Sampling of Bayesian Networks

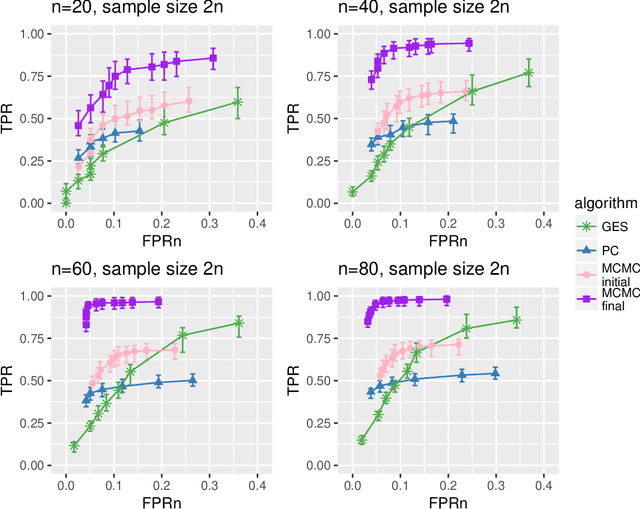
Bayesian networks are probabilistic graphical models widely employed to understand dependencies in high dimensional data, and even to facilitate causal discovery. Learning the underlying network structure, which is encoded as a directed acyclic graph (DAG) is highly challenging mainly due to the vast number of possible networks. Efforts have focussed on two fronts: constraint based methods that perform conditional independence tests to exclude edges and score and search approaches which explore the DAG space with greedy or MCMC schemes. Here we synthesise these two fields in a novel hybrid method which reduces the complexity of MCMC approaches to that of a constraint based method. Individual steps in the MCMC scheme only require simple table lookups so that very long chains can be efficiently obtained. Furthermore, the scheme includes an iterative procedure to correct for errors from the conditional independence tests. The algorithm not only offers markedly superior performance to alternatives, but DAGs can also be sampled from the posterior distribution enabling full Bayesian modelling averaging for much larger Bayesian networks.