Bayesian Causal Inference with Gaussian Process Networks
Paper and Code
Feb 01, 2024
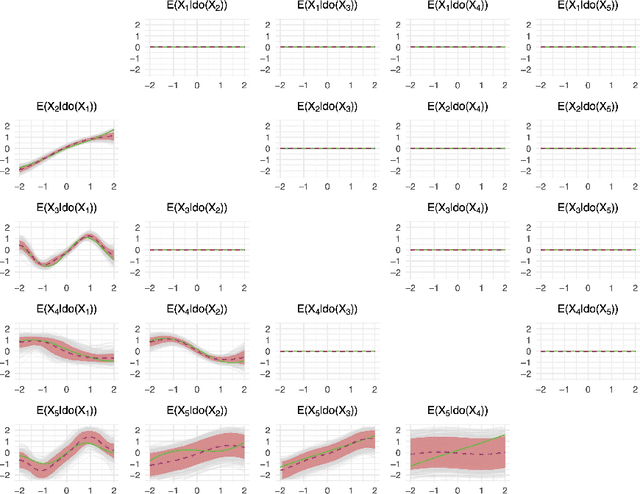
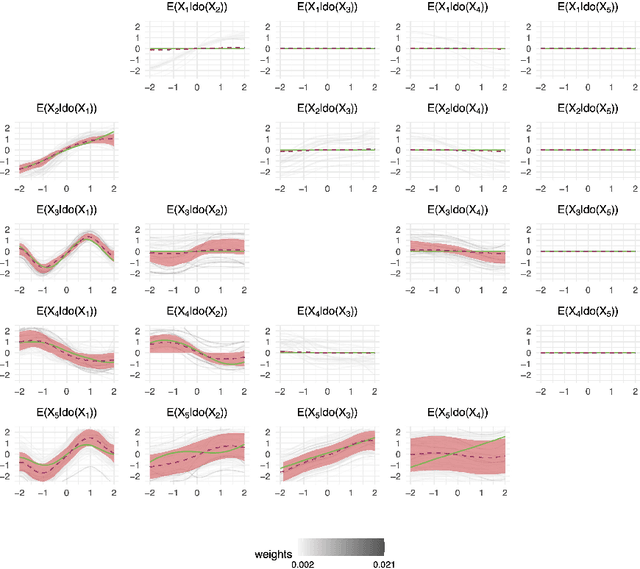

Causal discovery and inference from observational data is an essential problem in statistics posing both modeling and computational challenges. These are typically addressed by imposing strict assumptions on the joint distribution such as linearity. We consider the problem of the Bayesian estimation of the effects of hypothetical interventions in the Gaussian Process Network (GPN) model, a flexible causal framework which allows describing the causal relationships nonparametrically. We detail how to perform causal inference on GPNs by simulating the effect of an intervention across the whole network and propagating the effect of the intervention on downstream variables. We further derive a simpler computational approximation by estimating the intervention distribution as a function of local variables only, modeling the conditional distributions via additive Gaussian processes. We extend both frameworks beyond the case of a known causal graph, incorporating uncertainty about the causal structure via Markov chain Monte Carlo methods. Simulation studies show that our approach is able to identify the effects of hypothetical interventions with non-Gaussian, non-linear observational data and accurately reflect the posterior uncertainty of the causal estimates. Finally we compare the results of our GPN-based causal inference approach to existing methods on a dataset of $A.~thaliana$ gene expressions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge