Exact discovery is polynomial for sparse causal Bayesian networks

Causal Bayesian networks are widely used tools for summarising the dependencies between variables and elucidating their putative causal relationships. Learning networks from data is computationally hard in general. The current state-of-the-art approaches for exact causal discovery are integer linear programming over the underlying space of directed acyclic graphs, dynamic programming and shortest-path searches over the space of topological orders, and constraint programming combining both. For dynamic programming over orders, the computational complexity is known to be exponential base 2 in the number of variables in the network. We demonstrate how to use properties of Bayesian networks to prune the search space and lower the computational cost, while still guaranteeing exact discovery. When including new path-search and divide-and-conquer criteria, we prove optimality in quadratic time for matchings, and polynomial time for any network class with logarithmically-bound largest connected components. In simulation studies we observe the polynomial dependence for sparse networks and that, beyond some critical value, the logarithm of the base grows with the network density. Our approach then out-competes the state-of-the-art at lower densities. These results therefore pave the way for faster exact causal discovery in larger and sparser networks.

Benchpress: a scalable and platform-independent workflow for benchmarking structure learning algorithms for graphical models

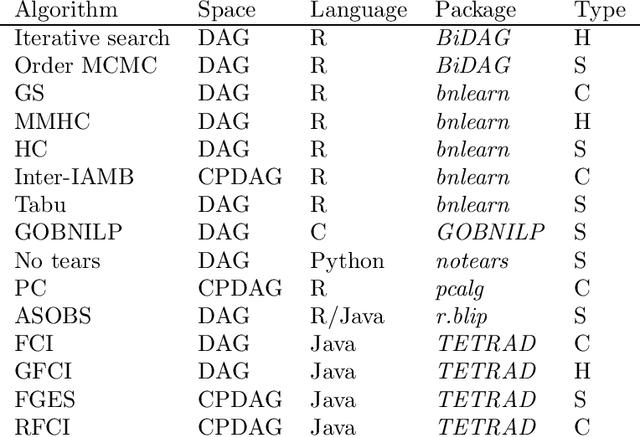
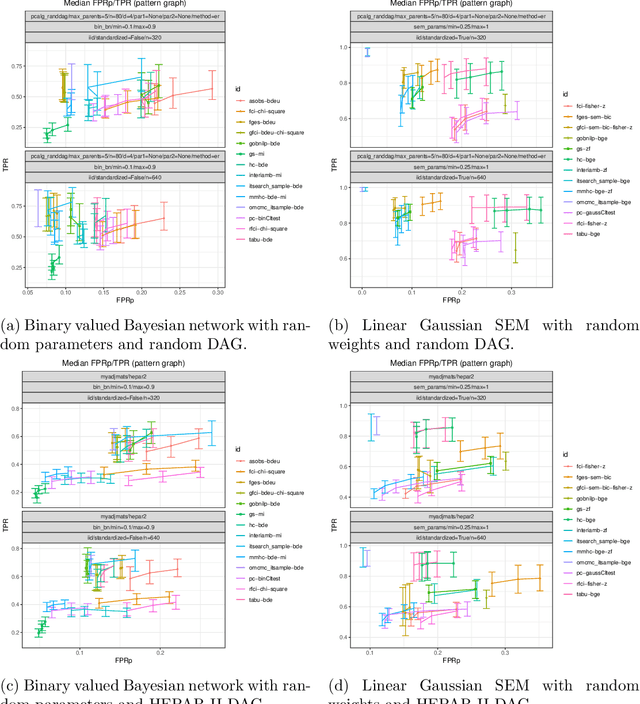
Describing the relationship between the variables in a study domain and modelling the data generating mechanism is a fundamental problem in many empirical sciences. Probabilistic graphical models are one common approach to tackle the problem. Learning the graphical structure is computationally challenging and a fervent area of current research with a plethora of algorithms being developed. To facilitate the benchmarking of different methods, we present a novel automated workflow, called benchpress for producing scalable, reproducible, and platform-independent benchmarks of structure learning algorithms for probabilistic graphical models. Benchpress is interfaced via a simple JSON-file, which makes it accessible for all users, while the code is designed in a fully modular fashion to enable researchers to contribute additional methodologies. Benchpress currently provides an interface to a large number of state-of-the-art algorithms from libraries such as BiDAG, bnlearn, GOBNILP, pcalg, r.blip, scikit-learn, TETRAD, and trilearn as well as a variety of methods for data generating models and performance evaluation. Alongside user-defined models and randomly generated datasets, the software tool also includes a number of standard datasets and graphical models from the literature, which may be included in a benchmarking workflow. We demonstrate the applicability of this workflow for learning Bayesian networks in four typical data scenarios. The source code and documentation is publicly available from http://github.com/felixleopoldo/benchpress.

A Prior Distribution over Directed Acyclic Graphs for Sparse Bayesian Networks

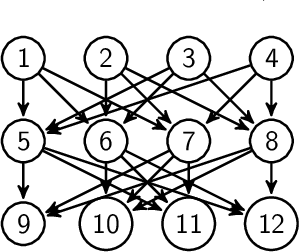
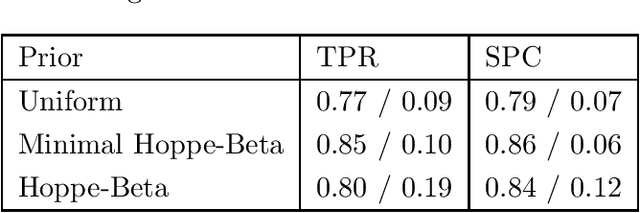
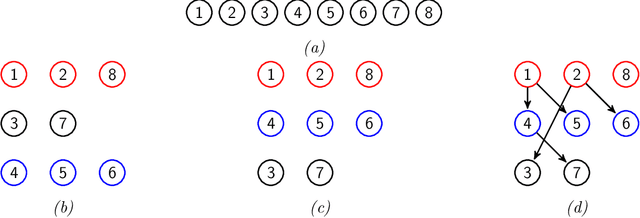
The main contribution of this article is a new prior distribution over directed acyclic graphs, which gives larger weight to sparse graphs. This distribution is intended for structured Bayesian networks, where the structure is given by an ordered block model. That is, the nodes of the graph are objects which fall into categories (or blocks); the blocks have a natural ordering. The presence of a relationship between two objects is denoted by an arrow, from the object of lower category to the object of higher category. The models considered here were introduced in Kemp et al. (2004) for relational data and extended to multivariate data in Mansinghka et al. (2006). The prior over graph structures presented here has an explicit formula. The number of nodes in each layer of the graph follow a Hoppe Ewens urn model. We consider the situation where the nodes of the graph represent random variables, whose joint probability distribution factorises along the DAG. We describe Monte Carlo schemes for finding the optimal aposteriori structure given a data matrix and compare the performance with Mansinghka et al. (2006) and also with the uniform prior.