John M. Noble
A Prior Distribution over Directed Acyclic Graphs for Sparse Bayesian Networks
Apr 25, 2015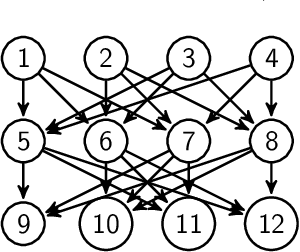
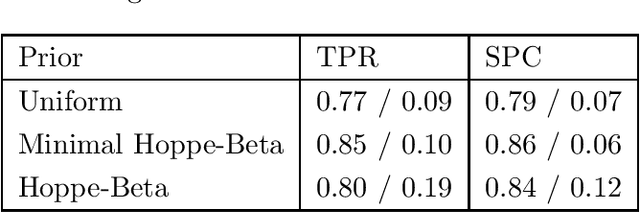
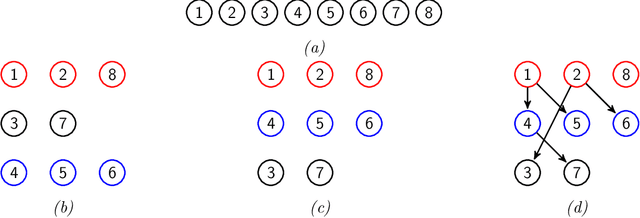
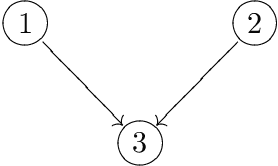
Abstract:The main contribution of this article is a new prior distribution over directed acyclic graphs, which gives larger weight to sparse graphs. This distribution is intended for structured Bayesian networks, where the structure is given by an ordered block model. That is, the nodes of the graph are objects which fall into categories (or blocks); the blocks have a natural ordering. The presence of a relationship between two objects is denoted by an arrow, from the object of lower category to the object of higher category. The models considered here were introduced in Kemp et al. (2004) for relational data and extended to multivariate data in Mansinghka et al. (2006). The prior over graph structures presented here has an explicit formula. The number of nodes in each layer of the graph follow a Hoppe Ewens urn model. We consider the situation where the nodes of the graph represent random variables, whose joint probability distribution factorises along the DAG. We describe Monte Carlo schemes for finding the optimal aposteriori structure given a data matrix and compare the performance with Mansinghka et al. (2006) and also with the uniform prior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge