On the Identifiability and Estimation of Causal Location-Scale Noise Models
Paper and Code
Oct 13, 2022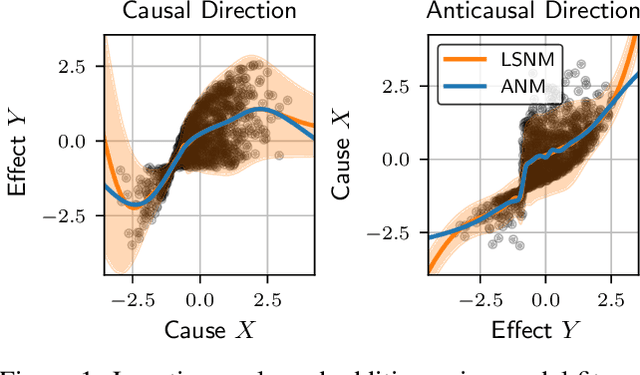
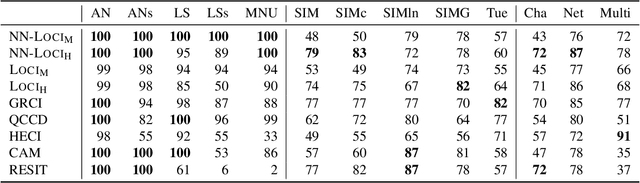
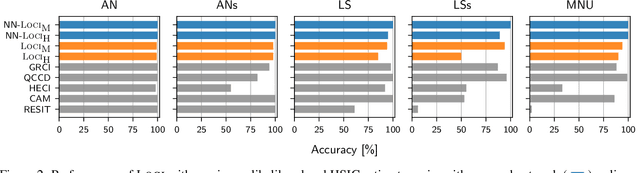
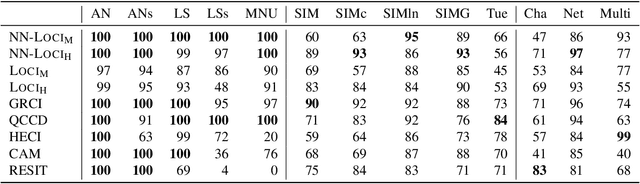
We study the class of location-scale or heteroscedastic noise models (LSNMs), in which the effect $Y$ can be written as a function of the cause $X$ and a noise source $N$ independent of $X$, which may be scaled by a positive function $g$ over the cause, i.e., $Y = f(X) + g(X)N$. Despite the generality of the model class, we show the causal direction is identifiable up to some pathological cases. To empirically validate these theoretical findings, we propose two estimators for LSNMs: an estimator based on (non-linear) feature maps, and one based on probabilistic neural networks. Both model the conditional distribution of $Y$ given $X$ as a Gaussian parameterized by its natural parameters. Since the neural network approach can fit functions of arbitrary complexity, it has an edge over the feature map-based approach in terms of empirical performance. When the feature maps are correctly specified, however, we can prove that our estimator is jointly concave, which allows us to derive stronger guarantees for the cause-effect identification task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge