A Weaker Faithfulness Assumption based on Triple Interactions

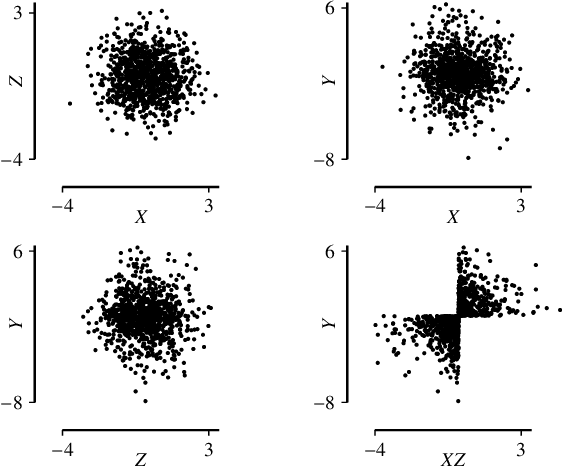
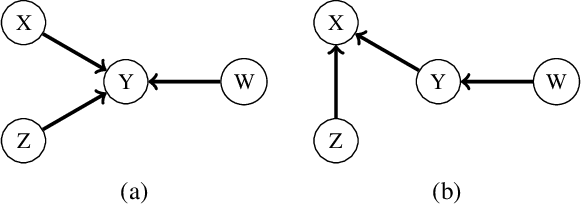
One of the core assumptions in causal discovery is the faithfulness assumption---i.e. assuming that independencies found in the data are due to separations in the true causal graph. This assumption can, however, be violated in many ways, including xor connections, deterministic functions or cancelling paths. In this work, we propose a weaker assumption that we call 2-adjacency faithfulness. In contrast to adjacency faithfulness, which assumes that there is no conditional independence between each pair of variables that are connected in the causal graph, we only require no conditional independence between a node and a subset of its Markov blanket that can contain up to two nodes. Equivalently, we adapt orientation faithfulness to this setting. We further propose a sound orientation rule for causal discovery that applies under weaker assumptions. As a proof of concept, we derive a modified Grow and Shrink algorithm that recovers the Markov blanket of a target node and prove its correctness under strictly weaker assumptions than the standard faithfulness assumption.