From Parameters to Behavior: Unsupervised Compression of the Policy Space

Despite its recent successes, Deep Reinforcement Learning (DRL) is notoriously sample-inefficient. We argue that this inefficiency stems from the standard practice of optimizing policies directly in the high-dimensional and highly redundant parameter space $\Theta$. This challenge is greatly compounded in multi-task settings. In this work, we develop a novel, unsupervised approach that compresses the policy parameter space $\Theta$ into a low-dimensional latent space $\mathcal{Z}$. We train a generative model $g:\mathcal{Z}\to\Theta$ by optimizing a behavioral reconstruction loss, which ensures that the latent space is organized by functional similarity rather than proximity in parameterization. We conjecture that the inherent dimensionality of this manifold is a function of the environment's complexity, rather than the size of the policy network. We validate our approach in continuous control domains, showing that the parameterization of standard policy networks can be compressed up to five orders of magnitude while retaining most of its expressivity. As a byproduct, we show that the learned manifold enables task-specific adaptation via Policy Gradient operating in the latent space $\mathcal{Z}$.

State Entropy Regularization for Robust Reinforcement Learning

State entropy regularization has empirically shown better exploration and sample complexity in reinforcement learning (RL). However, its theoretical guarantees have not been studied. In this paper, we show that state entropy regularization improves robustness to structured and spatially correlated perturbations. These types of variation are common in transfer learning but often overlooked by standard robust RL methods, which typically focus on small, uncorrelated changes. We provide a comprehensive characterization of these robustness properties, including formal guarantees under reward and transition uncertainty, as well as settings where the method performs poorly. Much of our analysis contrasts state entropy with the widely used policy entropy regularization, highlighting their different benefits. Finally, from a practical standpoint, we illustrate that compared with policy entropy, the robustness advantages of state entropy are more sensitive to the number of rollouts used for policy evaluation.

Enhancing Diversity in Parallel Agents: A Maximum State Entropy Exploration Story

Parallel data collection has redefined Reinforcement Learning (RL), unlocking unprecedented efficiency and powering breakthroughs in large-scale real-world applications. In this paradigm, $N$ identical agents operate in $N$ replicas of an environment simulator, accelerating data collection by a factor of $N$. A critical question arises: \textit{Does specializing the policies of the parallel agents hold the key to surpass the $N$ factor acceleration?} In this paper, we introduce a novel learning framework that maximizes the entropy of collected data in a parallel setting. Our approach carefully balances the entropy of individual agents with inter-agent diversity, effectively minimizing redundancies. The latter idea is implemented with a centralized policy gradient method, which shows promise when evaluated empirically against systems of identical agents, as well as synergy with batch RL techniques that can exploit data diversity. Finally, we provide an original concentration analysis that shows faster rates for specialized parallel sampling distributions, which supports our methodology and may be of independent interest.

A Classification View on Meta Learning Bandits

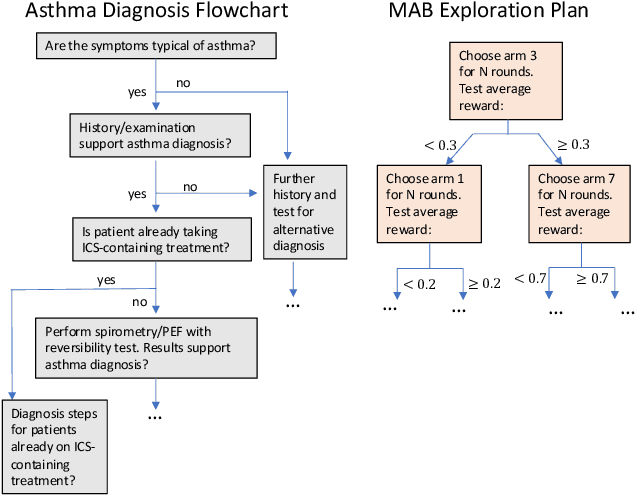
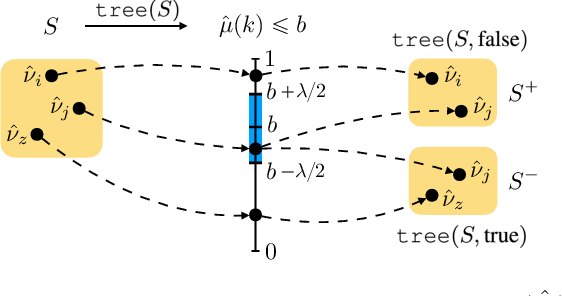
Contextual multi-armed bandits are a popular choice to model sequential decision-making. E.g., in a healthcare application we may perform various tests to asses a patient condition (exploration) and then decide on the best treatment to give (exploitation). When humans design strategies, they aim for the exploration to be fast, since the patient's health is at stake, and easy to interpret for a physician overseeing the process. However, common bandit algorithms are nothing like that: The regret caused by exploration scales with $\sqrt{H}$ over $H$ rounds and decision strategies are based on opaque statistical considerations. In this paper, we use an original classification view to meta learn interpretable and fast exploration plans for a fixed collection of bandits $\mathbb{M}$. The plan is prescribed by an interpretable decision tree probing decisions' payoff to classify the test bandit. The test regret of the plan in the stochastic and contextual setting scales with $O (\lambda^{-2} C_{\lambda} (\mathbb{M}) \log^2 (MH))$, being $M$ the size of $\mathbb{M}$, $\lambda$ a separation parameter over the bandits, and $C_\lambda (\mathbb{M})$ a novel classification-coefficient that fundamentally links meta learning bandits with classification. Through a nearly matching lower bound, we show that $C_\lambda (\mathbb{M})$ inherently captures the complexity of the setting.

Towards Principled Multi-Agent Task Agnostic Exploration

In reinforcement learning, we typically refer to task-agnostic exploration when we aim to explore the environment without access to the task specification a priori. In a single-agent setting the problem has been extensively studied and mostly understood. A popular approach cast the task-agnostic objective as maximizing the entropy of the state distribution induced by the agent's policy, from which principles and methods follows. In contrast, little is known about task-agnostic exploration in multi-agent settings, which are ubiquitous in the real world. How should different agents explore in the presence of others? In this paper, we address this question through a generalization to multiple agents of the problem of maximizing the state distribution entropy. First, we investigate alternative formulations, highlighting respective positives and negatives. Then, we present a scalable, decentralized, trust-region policy search algorithm to address the problem in practical settings. Finally, we provide proof of concept experiments to both corroborate the theoretical findings and pave the way for task-agnostic exploration in challenging multi-agent settings.

Reward Compatibility: A Framework for Inverse RL

We provide an original theoretical study of Inverse Reinforcement Learning (IRL) through the lens of reward compatibility, a novel framework to quantify the compatibility of a reward with the given expert's demonstrations. Intuitively, a reward is more compatible with the demonstrations the closer the performance of the expert's policy computed with that reward is to the optimal performance for that reward. This generalizes the notion of feasible reward set, the most common framework in the theoretical IRL literature, for which a reward is either compatible or not compatible. The grayscale introduced by the reward compatibility is the key to extend the realm of provably efficient IRL far beyond what is attainable with the feasible reward set: from tabular to large-scale MDPs. We analyze the IRL problem across various settings, including optimal and suboptimal expert's demonstrations and both online and offline data collection. For all of these dimensions, we provide a tractable algorithm and corresponding sample complexity analysis, as well as various insights on reward compatibility and how the framework can pave the way to yet more general problem settings.

Geometric Active Exploration in Markov Decision Processes: the Benefit of Abstraction

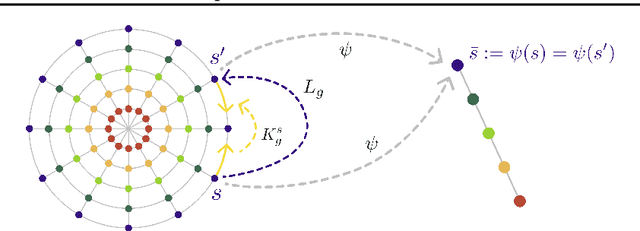
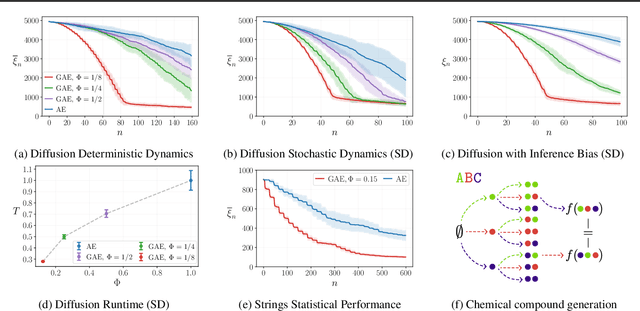
How can a scientist use a Reinforcement Learning (RL) algorithm to design experiments over a dynamical system's state space? In the case of finite and Markovian systems, an area called Active Exploration (AE) relaxes the optimization problem of experiments design into Convex RL, a generalization of RL admitting a wider notion of reward. Unfortunately, this framework is currently not scalable and the potential of AE is hindered by the vastness of experiment spaces typical of scientific discovery applications. However, these spaces are often endowed with natural geometries, e.g., permutation invariance in molecular design, that an agent could leverage to improve the statistical and computational efficiency of AE. To achieve this, we bridge AE and MDP homomorphisms, which offer a way to exploit known geometric structures via abstraction. Towards this goal, we make two fundamental contributions: we extend MDP homomorphisms formalism to Convex RL, and we present, to the best of our knowledge, the first analysis that formally captures the benefit of abstraction via homomorphisms on sample efficiency. Ultimately, we propose the Geometric Active Exploration (GAE) algorithm, which we analyse theoretically and experimentally in environments motivated by problems in scientific discovery.

The Limits of Pure Exploration in POMDPs: When the Observation Entropy is Enough

The problem of pure exploration in Markov decision processes has been cast as maximizing the entropy over the state distribution induced by the agent's policy, an objective that has been extensively studied. However, little attention has been dedicated to state entropy maximization under partial observability, despite the latter being ubiquitous in applications, e.g., finance and robotics, in which the agent only receives noisy observations of the true state governing the system's dynamics. How can we address state entropy maximization in those domains? In this paper, we study the simple approach of maximizing the entropy over observations in place of true latent states. First, we provide lower and upper bounds to the approximation of the true state entropy that only depends on some properties of the observation function. Then, we show how knowledge of the latter can be exploited to compute a principled regularization of the observation entropy to improve performance. With this work, we provide both a flexible approach to bring advances in state entropy maximization to the POMDP setting and a theoretical characterization of its intrinsic limits.

How to Scale Inverse RL to Large State Spaces? A Provably Efficient Approach

In online Inverse Reinforcement Learning (IRL), the learner can collect samples about the dynamics of the environment to improve its estimate of the reward function. Since IRL suffers from identifiability issues, many theoretical works on online IRL focus on estimating the entire set of rewards that explain the demonstrations, named the feasible reward set. However, none of the algorithms available in the literature can scale to problems with large state spaces. In this paper, we focus on the online IRL problem in Linear Markov Decision Processes (MDPs). We show that the structure offered by Linear MDPs is not sufficient for efficiently estimating the feasible set when the state space is large. As a consequence, we introduce the novel framework of rewards compatibility, which generalizes the notion of feasible set, and we develop CATY-IRL, a sample efficient algorithm whose complexity is independent of the cardinality of the state space in Linear MDPs. When restricted to the tabular setting, we demonstrate that CATY-IRL is minimax optimal up to logarithmic factors. As a by-product, we show that Reward-Free Exploration (RFE) enjoys the same worst-case rate, improving over the state-of-the-art lower bound. Finally, we devise a unifying framework for IRL and RFE that may be of independent interest.

How to Explore with Belief: State Entropy Maximization in POMDPs

Recent works have studied *state entropy maximization* in reinforcement learning, in which the agent's objective is to learn a policy inducing high entropy over states visitation (Hazan et al., 2019). They typically assume full observability of the state of the system, so that the entropy of the observations is maximized. In practice, the agent may only get *partial* observations, e.g., a robot perceiving the state of a physical space through proximity sensors and cameras. A significant mismatch between the entropy over observations and true states of the system can arise in those settings. In this paper, we address the problem of entropy maximization over the *true states* with a decision policy conditioned on partial observations *only*. The latter is a generalization of POMDPs, which is intractable in general. We develop a memory and computationally efficient *policy gradient* method to address a first-order relaxation of the objective defined on *belief* states, providing various formal characterizations of approximation gaps, the optimization landscape, and the *hallucination* problem. This paper aims to generalize state entropy maximization to more realistic domains that meet the challenges of applications.