Lambda-Skip Connections: the architectural component that prevents Rank Collapse

Rank collapse, a phenomenon where embedding vectors in sequence models rapidly converge to a uniform token or equilibrium state, has recently gained attention in the deep learning literature. This phenomenon leads to reduced expressivity and potential training instabilities due to vanishing gradients. Empirical evidence suggests that architectural components like skip connections, LayerNorm, and MultiLayer Perceptrons (MLPs) play critical roles in mitigating rank collapse. While this issue is well-documented for transformers, alternative sequence models, such as State Space Models (SSMs), which have recently gained prominence, have not been thoroughly examined for similar vulnerabilities. This paper extends the theory of rank collapse from transformers to SSMs using a unifying framework that captures both architectures. We study how a parametrized version of the classic skip connection component, which we call \emph{lambda-skip connections}, provides guarantees for rank collapse prevention. Through analytical results, we present a sufficient condition to guarantee prevention of rank collapse across all the aforementioned architectures. We also study the necessity of this condition via ablation studies and analytical examples. To our knowledge, this is the first study that provides a general guarantee to prevent rank collapse, and that investigates rank collapse in the context of SSMs, offering valuable understanding for both theoreticians and practitioners. Finally, we validate our findings with experiments demonstrating the crucial role of architectural components such as skip connections and gating mechanisms in preventing rank collapse.

Geometric Active Exploration in Markov Decision Processes: the Benefit of Abstraction

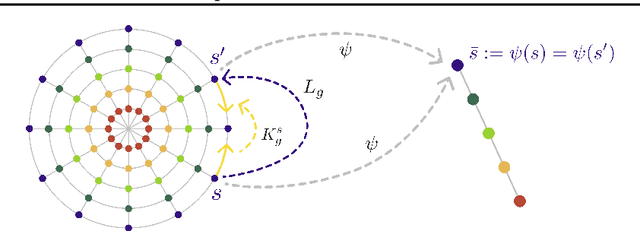
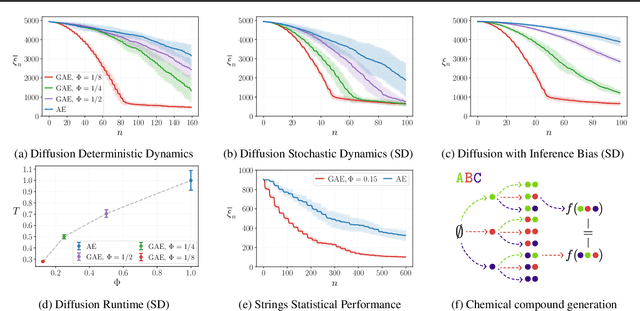
How can a scientist use a Reinforcement Learning (RL) algorithm to design experiments over a dynamical system's state space? In the case of finite and Markovian systems, an area called Active Exploration (AE) relaxes the optimization problem of experiments design into Convex RL, a generalization of RL admitting a wider notion of reward. Unfortunately, this framework is currently not scalable and the potential of AE is hindered by the vastness of experiment spaces typical of scientific discovery applications. However, these spaces are often endowed with natural geometries, e.g., permutation invariance in molecular design, that an agent could leverage to improve the statistical and computational efficiency of AE. To achieve this, we bridge AE and MDP homomorphisms, which offer a way to exploit known geometric structures via abstraction. Towards this goal, we make two fundamental contributions: we extend MDP homomorphisms formalism to Convex RL, and we present, to the best of our knowledge, the first analysis that formally captures the benefit of abstraction via homomorphisms on sample efficiency. Ultimately, we propose the Geometric Active Exploration (GAE) algorithm, which we analyse theoretically and experimentally in environments motivated by problems in scientific discovery.

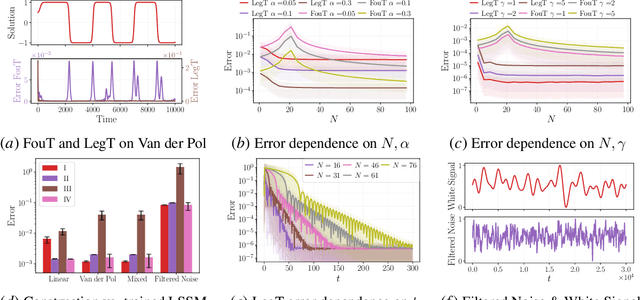
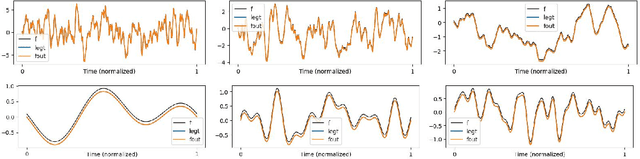
HiPPO-Prophecy: State-Space Models can Provably Learn Dynamical Systems in Context

This work explores the in-context learning capabilities of State Space Models (SSMs) and presents, to the best of our knowledge, the first theoretical explanation of a possible underlying mechanism. We introduce a novel weight construction for SSMs, enabling them to predict the next state of any dynamical system after observing previous states without parameter fine-tuning. This is accomplished by extending the HiPPO framework to demonstrate that continuous SSMs can approximate the derivative of any input signal. Specifically, we find an explicit weight construction for continuous SSMs and provide an asymptotic error bound on the derivative approximation. The discretization of this continuous SSM subsequently yields a discrete SSM that predicts the next state. Finally, we demonstrate the effectiveness of our parameterization empirically. This work should be an initial step toward understanding how sequence models based on SSMs learn in context.