Continuous Relaxation For The Multivariate Non-Central Hypergeometric Distribution

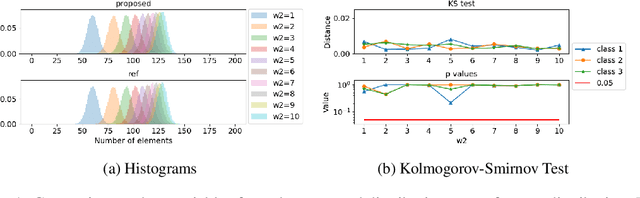
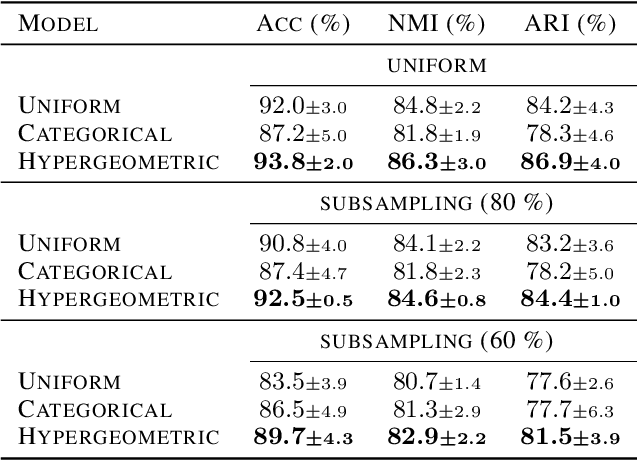
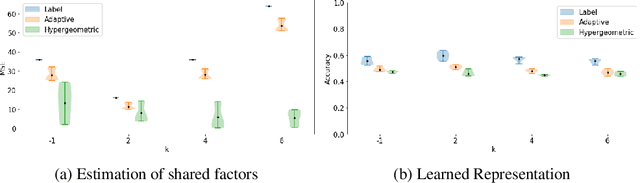
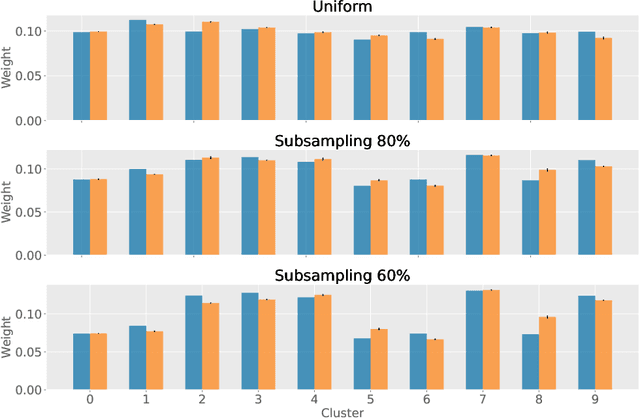
Partitioning a set of elements into a given number of groups of a priori unknown sizes is an important task in many applications. Due to hard constraints, it is a non-differentiable problem which prohibits its direct use in modern machine learning frameworks. Hence, previous works mostly fall back on suboptimal heuristics or simplified assumptions. The multivariate hypergeometric distribution offers a probabilistic formulation of how to distribute a given number of samples across multiple groups. Unfortunately, as a discrete probability distribution, it neither is differentiable. In this work, we propose a continuous relaxation for the multivariate non-central hypergeometric distribution. We introduce an efficient and numerically stable sampling procedure. This enables reparameterized gradients for the hypergeometric distribution and its integration into automatic differentiation frameworks. We highlight the applicability and usability of the proposed formulation on two different common machine learning tasks.