Stochastic Causal Programming for Bounding Treatment Effects
Paper and Code
Feb 22, 2022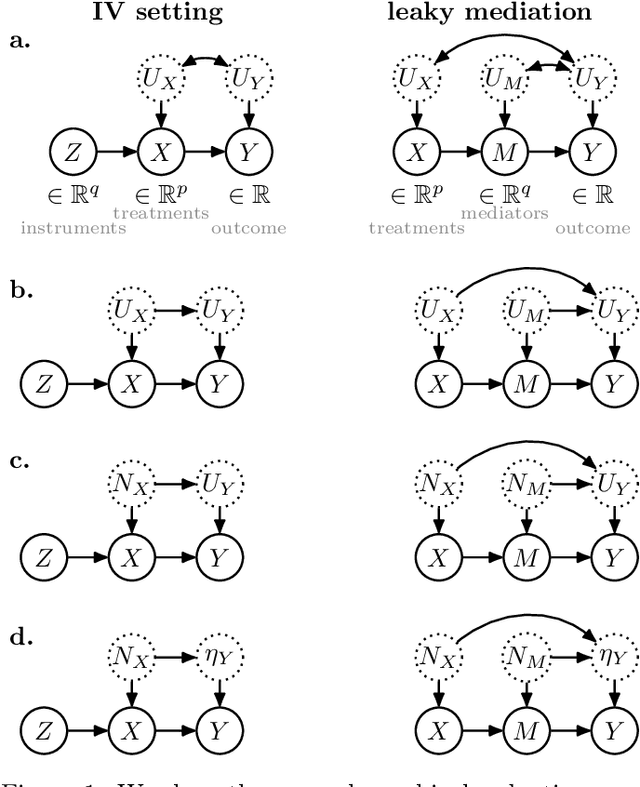
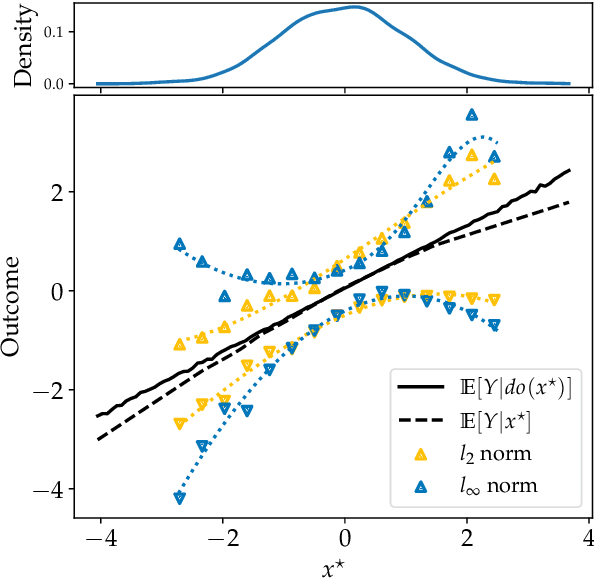
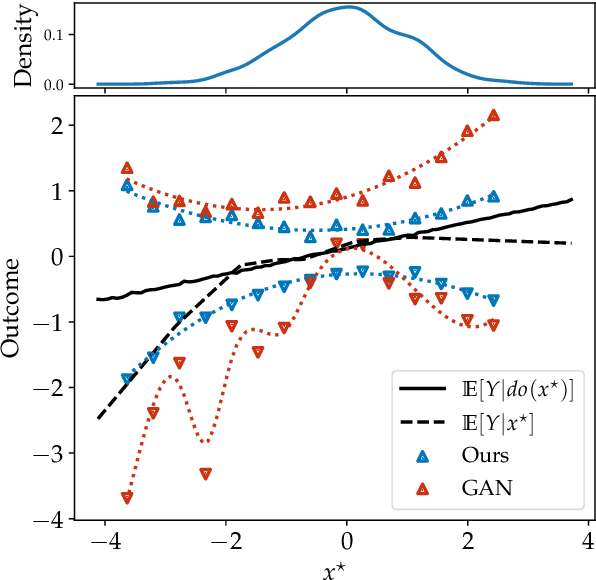
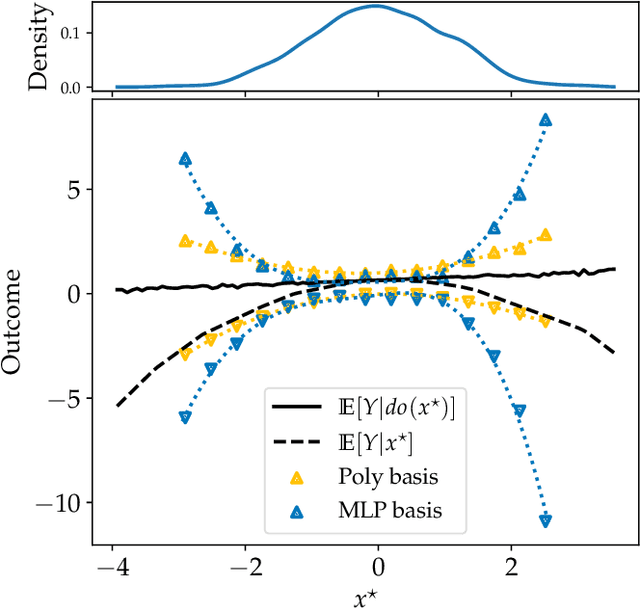
Causal effect estimation is important for numerous tasks in the natural and social sciences. However, identifying effects is impossible from observational data without making strong, often untestable assumptions. We consider algorithms for the partial identification problem, bounding treatment effects from multivariate, continuous treatments over multiple possible causal models when unmeasured confounding makes identification impossible. We consider a framework where observable evidence is matched to the implications of constraints encoded in a causal model by norm-based criteria. This generalizes classical approaches based purely on generative models. Casting causal effects as objective functions in a constrained optimization problem, we combine flexible learning algorithms with Monte Carlo methods to implement a family of solutions under the name of stochastic causal programming. In particular, we present ways by which such constrained optimization problems can be parameterized without likelihood functions for the causal or the observed data model, reducing the computational and statistical complexity of the task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge