Contrastive representations of high-dimensional, structured treatments

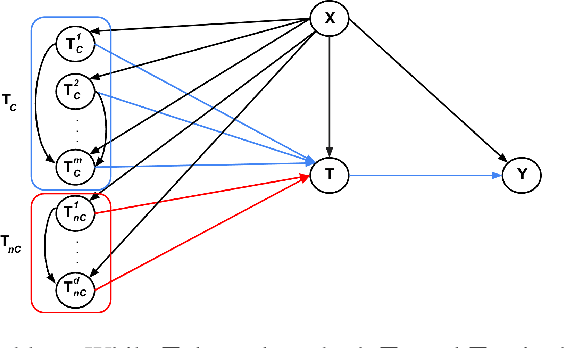
Estimating causal effects is vital for decision making. In standard causal effect estimation, treatments are usually binary- or continuous-valued. However, in many important real-world settings, treatments can be structured, high-dimensional objects, such as text, video, or audio. This provides a challenge to traditional causal effect estimation. While leveraging the shared structure across different treatments can help generalize to unseen treatments at test time, we show in this paper that using such structure blindly can lead to biased causal effect estimation. We address this challenge by devising a novel contrastive approach to learn a representation of the high-dimensional treatments, and prove that it identifies underlying causal factors and discards non-causally relevant factors. We prove that this treatment representation leads to unbiased estimates of the causal effect, and empirically validate and benchmark our results on synthetic and real-world datasets.

Non-parametric identifiability and sensitivity analysis of synthetic control models

Quantifying cause and effect relationships is an important problem in many domains. The gold standard solution is to conduct a randomised controlled trial. However, in many situations such trials cannot be performed. In the absence of such trials, many methods have been devised to quantify the causal impact of an intervention from observational data given certain assumptions. One widely used method are synthetic control models. While identifiability of the causal estimand in such models has been obtained from a range of assumptions, it is widely and implicitly assumed that the underlying assumptions are satisfied for all time periods both pre- and post-intervention. This is a strong assumption, as synthetic control models can only be learned in pre-intervention period. In this paper we address this challenge, and prove identifiability can be obtained without the need for this assumption, by showing it follows from the principle of invariant causal mechanisms. Moreover, for the first time, we formulate and study synthetic control models in Pearl's structural causal model framework. Importantly, we provide a general framework for sensitivity analysis of synthetic control causal inference to violations of the assumptions underlying non-parametric identifiability. We end by providing an empirical demonstration of our sensitivity analysis framework on simulated and real data in the widely-used linear synthetic control framework.

Estimating the probabilities of causation via deep monotonic twin networks

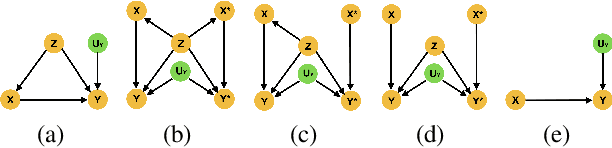
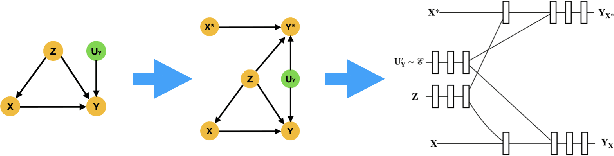
There has been much recent work using machine learning to answer causal queries. Most focus on interventional queries, such as the conditional average treatment effect. However, as noted by Pearl, interventional queries only form part of a larger hierarchy of causal queries, with counterfactuals sitting at the top. Despite this, our community has not fully succeeded in adapting machine learning tools to answer counterfactual queries. This work addresses this challenge by showing how to implement twin network counterfactual inference -- an alternative to abduction, action, & prediction counterfactual inference -- with deep learning to estimate counterfactual queries. We show how the graphical nature of twin networks makes them particularly amenable to deep learning, yielding simple neural network architectures that, when trained, are capable of counterfactual inference. Importantly, we show how to enforce known identifiability constraints during training, ensuring the answer to each counterfactual query is uniquely determined. We demonstrate our approach by using it to accurately estimate the probabilities of causation -- important counterfactual queries that quantify the degree to which one event was a necessary or sufficient cause of another -- on both synthetic and real data.