The Causal Marginal Polytope for Bounding Treatment Effects
Paper and Code
Feb 28, 2022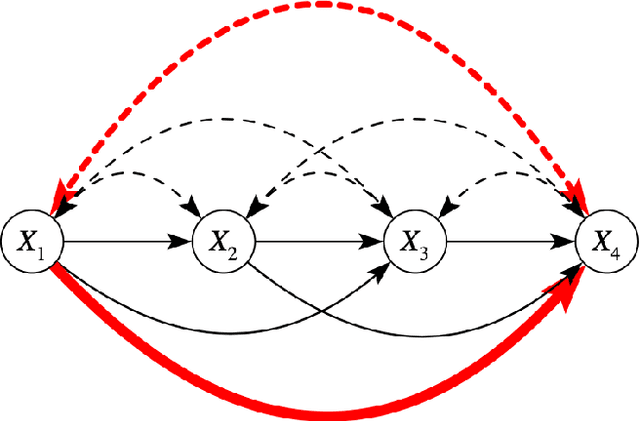
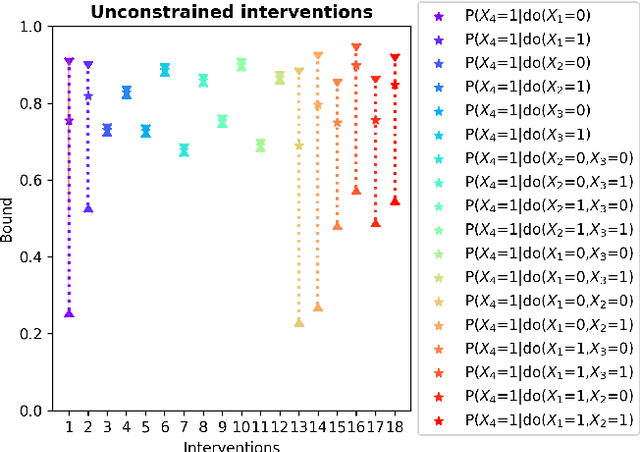
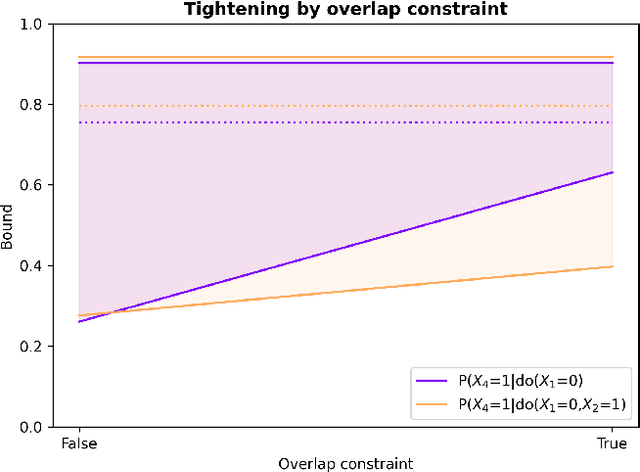
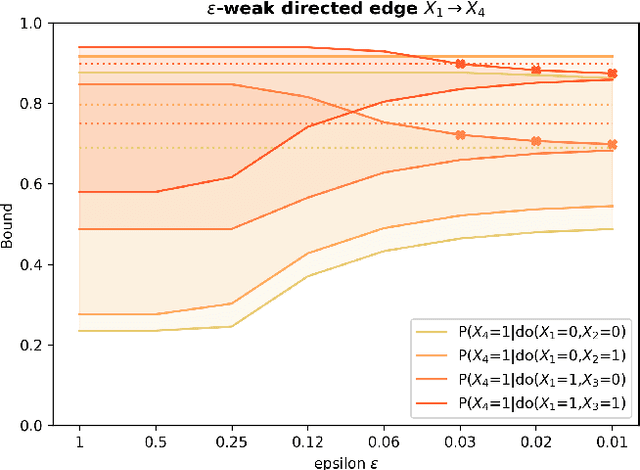
Due to unmeasured confounding, it is often not possible to identify causal effects from a postulated model. Nevertheless, we can ask for partial identification, which usually boils down to finding upper and lower bounds of a causal quantity of interest derived from all solutions compatible with the encoded structural assumptions. One appealing way to derive such bounds is by casting it in terms of a constrained optimization method that searches over all causal models compatible with evidence, as introduced in the classic work of Balke and Pearl (1994) for discrete data. Although by construction this guarantees tight bounds, it poses a formidable computational challenge. To cope with this issue, alternatives include algorithms that are not guaranteed to be tight, or by introducing restrictions on the class of models. In this paper, we introduce a novel alternative: inspired by ideas coming from belief propagation, we enforce compatibility between marginals of a causal model and data, without constructing a global causal model. We call this collection of locally consistent marginals the causal marginal polytope. As global independence constraints disappear when considering small dimensional tractable marginals, this also leads to a rethinking of how to elicit and express causal knowledge. We provide an explicit algorithm and implementation of this idea, and assess its practicality with numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge