Auditing a Dutch Public Sector Risk Profiling Algorithm Using an Unsupervised Bias Detection Tool

Algorithms are increasingly used to automate or aid human decisions, yet recent research shows that these algorithms may exhibit bias across legally protected demographic groups. However, data on these groups may be unavailable to organizations or external auditors due to privacy legislation. This paper studies bias detection using an unsupervised clustering tool when data on demographic groups are unavailable. We collaborate with the Dutch Executive Agency for Education to audit an algorithm that was used to assign risk scores to college students at the national level in the Netherlands between 2012-2023. Our audit covers more than 250,000 students from the whole country. The unsupervised clustering tool highlights known disparities between students with a non-European migration background and Dutch origin. Our contributions are three-fold: (1) we assess bias in a real-world, large-scale and high-stakes decision-making process by a governmental organization; (2) we use simulation studies to highlight potential pitfalls of using the unsupervised clustering tool to detect true bias when demographic group data are unavailable and provide recommendations for valid inferences; (3) we provide the unsupervised clustering tool in an open-source library. Our work serves as a starting point for a deliberative assessment by human experts to evaluate potential discrimination in algorithmic-supported decision-making processes.

Prune Sampling: a MCMC inference technique for discrete and deterministic Bayesian networks

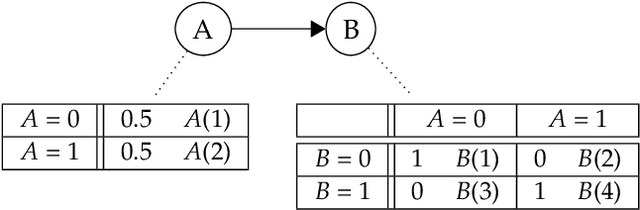
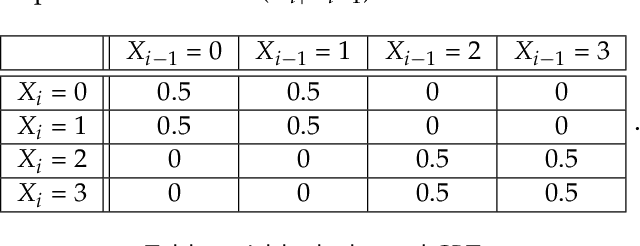
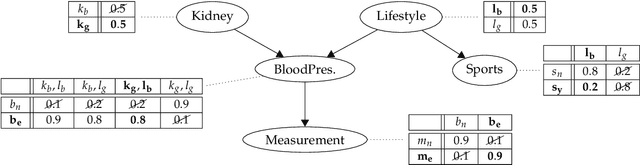
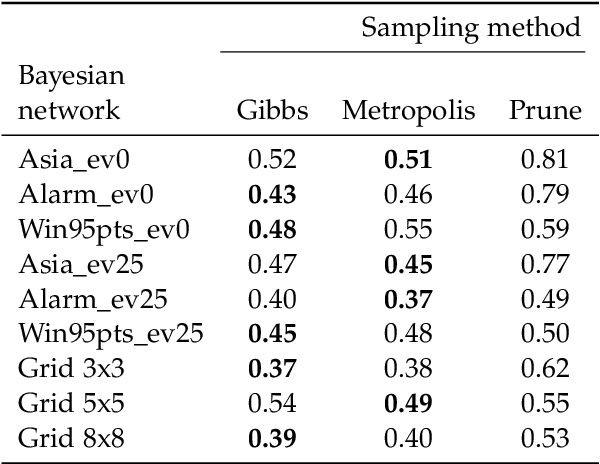
We introduce and characterise the performance of the Markov chain Monte Carlo (MCMC) inference method Prune Sampling for discrete and deterministic Bayesian networks (BNs). We developed a procedure to obtain the performance of a MCMC sampling method in the limit of infinite simulation time, extrapolated from relatively short simulations. This approach was used to conduct a study to compare the accuracy, rate of convergence and the time consumption of Prune Sampling with two conventional MCMC sampling methods: Gibbs- and Metropolis sampling. We show that Markov chains created by Prune Sampling always converge to the desired posterior distribution, also for networks where conventional Gibbs sampling fails. Beside this, we demonstrate that pruning outperforms Gibbs sampling, at least for a certain class of BNs. Though, this tempting feature comes at a price. In the first version of Prune Sampling, for large BNs the procedure to choose the next iteration step uniformly is rather time intensive. Our conclusion is that Prune Sampling is a competitive method for all types of small and medium sized BNs, but (for now) standard methods still perform better for all types of large BNs.