NeuralCrop: Combining physics and machine learning for improved crop yield predictions

Global gridded crop models (GGCMs) simulate daily crop growth by explicitly representing key biophysical processes and project end-of-season yield time series. They are a primary tool to quantify the impacts of climate change on agricultural productivity and assess associated risks for food security. Despite decades of development, state-of-the-art GGCMs still have substantial uncertainties in simulating complex biophysical processes due to limited process understanding. Recently, machine learning approaches trained on observational data have shown great potential in crop yield predictions. However, these models have not demonstrated improved performance over classical GGCMs and are not suitable for simulating crop yields under changing climate conditions due to problems in generalizing outside their training distributions. Here we introduce NeuralCrop, a hybrid GGCM that combines the strengths of an advanced process-based GGCM, resolving important processes explicitly, with data-driven machine learning components. The model is first trained to emulate a competitive GGCM before it is fine-tuned on observational data. We show that NeuralCrop outperforms state-of-the-art GGCMs across site-level and large-scale cropping regions. Across moisture conditions, NeuralCrop reproduces the interannual yield anomalies in European wheat regions and the US Corn Belt more accurately during the period from 2000 to 2019 with particularly strong improvements under drought extremes. When generalizing to conditions unseen during training, NeuralCrop continues to make robust projections, while pure machine learning models exhibit substantial performance degradation. Our results show that our hybrid crop modelling approach offers overall improved crop modeling and more reliable yield projections under climate change and intensifying extreme weather conditions.

Generating time-consistent dynamics with discriminator-guided image diffusion models

Realistic temporal dynamics are crucial for many video generation, processing and modelling applications, e.g. in computational fluid dynamics, weather prediction, or long-term climate simulations. Video diffusion models (VDMs) are the current state-of-the-art method for generating highly realistic dynamics. However, training VDMs from scratch can be challenging and requires large computational resources, limiting their wider application. Here, we propose a time-consistency discriminator that enables pretrained image diffusion models to generate realistic spatiotemporal dynamics. The discriminator guides the sampling inference process and does not require extensions or finetuning of the image diffusion model. We compare our approach against a VDM trained from scratch on an idealized turbulence simulation and a real-world global precipitation dataset. Our approach performs equally well in terms of temporal consistency, shows improved uncertainty calibration and lower biases compared to the VDM, and achieves stable centennial-scale climate simulations at daily time steps.

Improving the Noise Estimation of Latent Neural Stochastic Differential Equations

Latent neural stochastic differential equations (SDEs) have recently emerged as a promising approach for learning generative models from stochastic time series data. However, they systematically underestimate the noise level inherent in such data, limiting their ability to capture stochastic dynamics accurately. We investigate this underestimation in detail and propose a straightforward solution: by including an explicit additional noise regularization in the loss function, we are able to learn a model that accurately captures the diffusion component of the data. We demonstrate our results on a conceptual model system that highlights the improved latent neural SDE's capability to model stochastic bistable dynamics.

Projected Neural Differential Equations for Learning Constrained Dynamics

Neural differential equations offer a powerful approach for learning dynamics from data. However, they do not impose known constraints that should be obeyed by the learned model. It is well-known that enforcing constraints in surrogate models can enhance their generalizability and numerical stability. In this paper, we introduce projected neural differential equations (PNDEs), a new method for constraining neural differential equations based on projection of the learned vector field to the tangent space of the constraint manifold. In tests on several challenging examples, including chaotic dynamical systems and state-of-the-art power grid models, PNDEs outperform existing methods while requiring fewer hyperparameters. The proposed approach demonstrates significant potential for enhancing the modeling of constrained dynamical systems, particularly in complex domains where accuracy and reliability are essential.

Machine Learning for predicting chaotic systems

Predicting chaotic dynamical systems is critical in many scientific fields such as weather prediction, but challenging due to the characterizing sensitive dependence on initial conditions. Traditional modeling approaches require extensive domain knowledge, often leading to a shift towards data-driven methods using machine learning. However, existing research provides inconclusive results on which machine learning methods are best suited for predicting chaotic systems. In this paper, we compare different lightweight and heavyweight machine learning architectures using extensive existing databases, as well as a newly introduced one that allows for uncertainty quantification in the benchmark results. We perform hyperparameter tuning based on computational cost and introduce a novel error metric, the cumulative maximum error, which combines several desirable properties of traditional metrics, tailored for chaotic systems. Our results show that well-tuned simple methods, as well as untuned baseline methods, often outperform state-of-the-art deep learning models, but their performance can vary significantly with different experimental setups. These findings underscore the importance of matching prediction methods to data characteristics and available computational resources.

Stabilized Neural Differential Equations for Learning Constrained Dynamics

Many successful methods to learn dynamical systems from data have recently been introduced. However, assuring that the inferred dynamics preserve known constraints, such as conservation laws or restrictions on the allowed system states, remains challenging. We propose stabilized neural differential equations (SNDEs), a method to enforce arbitrary manifold constraints for neural differential equations. Our approach is based on a stabilization term that, when added to the original dynamics, renders the constraint manifold provably asymptotically stable. Due to its simplicity, our method is compatible with all common neural ordinary differential equation (NODE) models and broadly applicable. In extensive empirical evaluations, we demonstrate that SNDEs outperform existing methods while extending the scope of which types of constraints can be incorporated into NODE training.

Differentiable Programming for Earth System Modeling

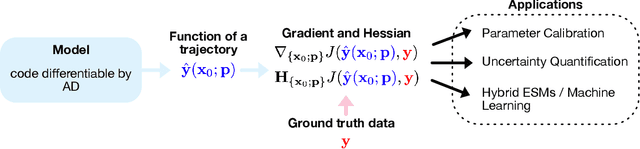
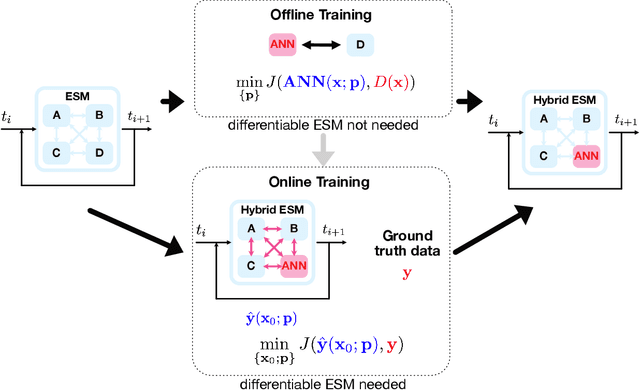
Earth System Models (ESMs) are the primary tools for investigating future Earth system states at time scales from decades to centuries, especially in response to anthropogenic greenhouse gas release. State-of-the-art ESMs can reproduce the observational global mean temperature anomalies of the last 150 years. Nevertheless, ESMs need further improvements, most importantly regarding (i) the large spread in their estimates of climate sensitivity, i.e., the temperature response to increases in atmospheric greenhouse gases, (ii) the modeled spatial patterns of key variables such as temperature and precipitation, (iii) their representation of extreme weather events, and (iv) their representation of multistable Earth system components and their ability to predict associated abrupt transitions. Here, we argue that making ESMs automatically differentiable has huge potential to advance ESMs, especially with respect to these key shortcomings. First, automatic differentiability would allow objective calibration of ESMs, i.e., the selection of optimal values with respect to a cost function for a large number of free parameters, which are currently tuned mostly manually. Second, recent advances in Machine Learning (ML) and in the amount, accuracy, and resolution of observational data promise to be helpful with at least some of the above aspects because ML may be used to incorporate additional information from observations into ESMs. Automatic differentiability is an essential ingredient in the construction of such hybrid models, combining process-based ESMs with ML components. We document recent work showcasing the potential of automatic differentiation for a new generation of substantially improved, data-informed ESMs.