Approximation of nearly-periodic symplectic maps via structure-preserving neural networks
Paper and Code
Oct 11, 2022
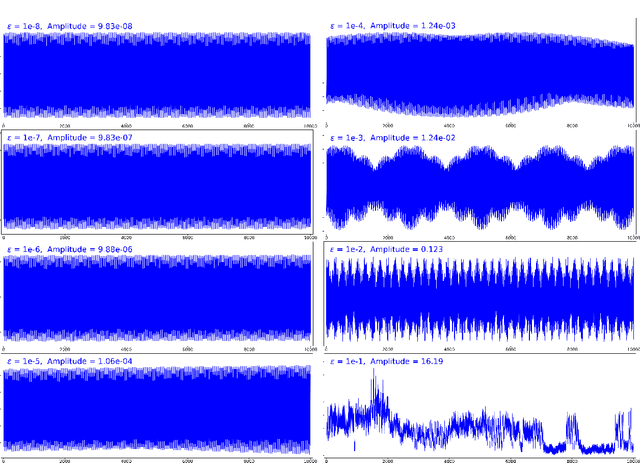

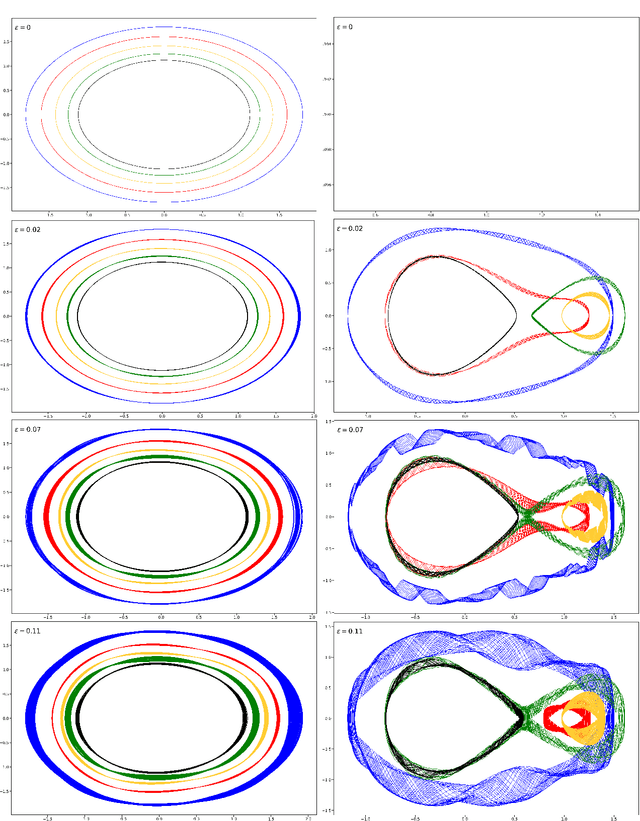
A continuous-time dynamical system with parameter $\varepsilon$ is nearly-periodic if all its trajectories are periodic with nowhere-vanishing angular frequency as $\varepsilon$ approaches 0. Nearly-periodic maps are discrete-time analogues of nearly-periodic systems, defined as parameter-dependent diffeomorphisms that limit to rotations along a circle action, and they admit formal $U(1)$ symmetries to all orders when the limiting rotation is non-resonant. For Hamiltonian nearly-periodic maps on exact presymplectic manifolds, the formal $U(1)$ symmetry gives rise to a discrete-time adiabatic invariant. In this paper, we construct a novel structure-preserving neural network to approximate nearly-periodic symplectic maps. This neural network architecture, which we call symplectic gyroceptron, ensures that the resulting surrogate map is nearly-periodic and symplectic, and that it gives rise to a discrete-time adiabatic invariant and a long-time stability. This new structure-preserving neural network provides a promising architecture for surrogate modeling of non-dissipative dynamical systems that automatically steps over short timescales without introducing spurious instabilities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge