Liouville Flow Importance Sampler

We present the Liouville Flow Importance Sampler (LFIS), an innovative flow-based model for generating samples from unnormalized density functions. LFIS learns a time-dependent velocity field that deterministically transports samples from a simple initial distribution to a complex target distribution, guided by a prescribed path of annealed distributions. The training of LFIS utilizes a unique method that enforces the structure of a derived partial differential equation to neural networks modeling velocity fields. By considering the neural velocity field as an importance sampler, sample weights can be computed through accumulating errors along the sample trajectories driven by neural velocity fields, ensuring unbiased and consistent estimation of statistical quantities. We demonstrate the effectiveness of LFIS through its application to a range of benchmark problems, on many of which LFIS achieved state-of-the-art performance.

Regression-based projection for learning Mori--Zwanzig operators

We propose to adopt statistical regression as the projection operator to enable data-driven learning of the operators in the Mori--Zwanzig formalism. We present a principled algorithm to extract the Markov and memory operators for any regression models. We show that the choice of linear regression results in a recently proposed data-driven learning algorithm based on Mori's projection operator, which can be considered as a higher-order approximate Koopman learning method. We show that more expressive, potentially nonlinear regression models naturally fill in the gap between the highly idealized and computationally efficient Mori's projection operator and the most optimal yet computationally infeasible Zwanzig projection operator. We performed numerical experiments and extracted the operators for an array of regression-based projections, including linear, polynomial, spline, and neural-network-based regression, showing a progressive improvement as the complexity of the regression model increased. Our proposition provides a general framework to extract memory-dependent corrections and can be readily applied to an array of data-driven learning methods for stationary dynamical systems in the literature.

Physics Informed Machine Learning of SPH: Machine Learning Lagrangian Turbulence

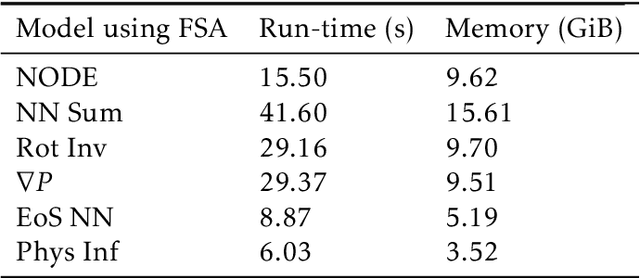
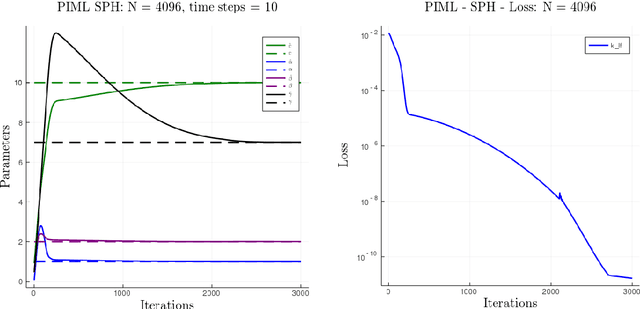
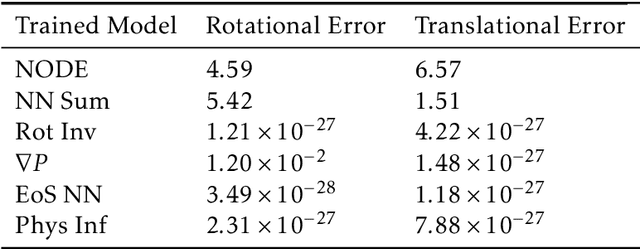
Smoothed particle hydrodynamics (SPH) is a mesh-free Lagrangian method for obtaining approximate numerical solutions of the equations of fluid dynamics; which has been widely applied to weakly- and strongly compressible turbulence in astrophysics and engineering applications. We present a learn-able hierarchy of parameterized and "physics-explainable" SPH informed fluid simulators using both physics based parameters and Neural Networks (NNs) as universal function approximators. Our learning algorithm develops a mixed mode approach, mixing forward and reverse mode automatic differentiation with forward and adjoint based sensitivity analyses to efficiently perform gradient based optimization. We show that our physics informed learning method is capable of: (a) solving inverse problems over the physically interpretable parameter space, as well as over the space of NN parameters; (b) learning Lagrangian statistics of turbulence (interpolation); (c) combining Lagrangian trajectory based, probabilistic, and Eulerian field based loss functions; and (d) extrapolating beyond training sets into more complex regimes of interest. Furthermore, this hierarchy of models gradually introduces more physical structure, which we show improves interpretability, generalizability (over larger ranges of time scales and Reynolds numbers), preservation of physical symmetries, and requires less training data.