Liouville Flow Importance Sampler

We present the Liouville Flow Importance Sampler (LFIS), an innovative flow-based model for generating samples from unnormalized density functions. LFIS learns a time-dependent velocity field that deterministically transports samples from a simple initial distribution to a complex target distribution, guided by a prescribed path of annealed distributions. The training of LFIS utilizes a unique method that enforces the structure of a derived partial differential equation to neural networks modeling velocity fields. By considering the neural velocity field as an importance sampler, sample weights can be computed through accumulating errors along the sample trajectories driven by neural velocity fields, ensuring unbiased and consistent estimation of statistical quantities. We demonstrate the effectiveness of LFIS through its application to a range of benchmark problems, on many of which LFIS achieved state-of-the-art performance.

Using Ornstein-Uhlenbeck Process to understand Denoising Diffusion Probabilistic Model and its Noise Schedules

The aim of this short note is to show that Denoising Diffusion Probabilistic Model DDPM, a non-homogeneous discrete-time Markov process, can be represented by a time-homogeneous continuous-time Markov process observed at non-uniformly sampled discrete times. Surprisingly, this continuous-time Markov process is the well-known and well-studied Ornstein-Ohlenbeck (OU) process, which was developed in 1930's for studying Brownian particles in Harmonic potentials. We establish the formal equivalence between DDPM and the OU process using its analytical solution. We further demonstrate that the design problem of the noise scheduler for non-homogeneous DDPM is equivalent to designing observation times for the OU process. We present several heuristic designs for observation times based on principled quantities such as auto-variance and Fisher Information and connect them to ad hoc noise schedules for DDPM. Interestingly, we show that the Fisher-Information-motivated schedule corresponds exactly the cosine schedule, which was developed without any theoretical foundation but is the current state-of-the-art noise schedule.

Improving Estimation of the Koopman Operator with Kolmogorov-Smirnov Indicator Functions

It has become common to perform kinetic analysis using approximate Koopman operators that transforms high-dimensional time series of observables into ranked dynamical modes. Key to a practical success of the approach is the identification of a set of observables which form a good basis in which to expand the slow relaxation modes. Good observables are, however, difficult to identify {\em a priori} and sub-optimal choices can lead to significant underestimations of characteristic timescales. Leveraging the representation of slow dynamics in terms of Hidden Markov Model (HMM), we propose a simple and computationally efficient clustering procedure to infer surrogate observables that form a good basis for slow modes. We apply the approach to an analytically solvable model system, as well as on three protein systems of different complexities. We consistently demonstrate that the inferred indicator functions can significantly improve the estimation of the leading eigenvalues of the Koopman operators and correctly identify key states and transition timescales of stochastic systems, even when good observables are not known {\em a priori}.

Blackout Diffusion: Generative Diffusion Models in Discrete-State Spaces

Typical generative diffusion models rely on a Gaussian diffusion process for training the backward transformations, which can then be used to generate samples from Gaussian noise. However, real world data often takes place in discrete-state spaces, including many scientific applications. Here, we develop a theoretical formulation for arbitrary discrete-state Markov processes in the forward diffusion process using exact (as opposed to variational) analysis. We relate the theory to the existing continuous-state Gaussian diffusion as well as other approaches to discrete diffusion, and identify the corresponding reverse-time stochastic process and score function in the continuous-time setting, and the reverse-time mapping in the discrete-time setting. As an example of this framework, we introduce ``Blackout Diffusion'', which learns to produce samples from an empty image instead of from noise. Numerical experiments on the CIFAR-10, Binarized MNIST, and CelebA datasets confirm the feasibility of our approach. Generalizing from specific (Gaussian) forward processes to discrete-state processes without a variational approximation sheds light on how to interpret diffusion models, which we discuss.

Regression-based projection for learning Mori--Zwanzig operators

We propose to adopt statistical regression as the projection operator to enable data-driven learning of the operators in the Mori--Zwanzig formalism. We present a principled algorithm to extract the Markov and memory operators for any regression models. We show that the choice of linear regression results in a recently proposed data-driven learning algorithm based on Mori's projection operator, which can be considered as a higher-order approximate Koopman learning method. We show that more expressive, potentially nonlinear regression models naturally fill in the gap between the highly idealized and computationally efficient Mori's projection operator and the most optimal yet computationally infeasible Zwanzig projection operator. We performed numerical experiments and extracted the operators for an array of regression-based projections, including linear, polynomial, spline, and neural-network-based regression, showing a progressive improvement as the complexity of the regression model increased. Our proposition provides a general framework to extract memory-dependent corrections and can be readily applied to an array of data-driven learning methods for stationary dynamical systems in the literature.

A phase transition for finding needles in nonlinear haystacks with LASSO artificial neural networks

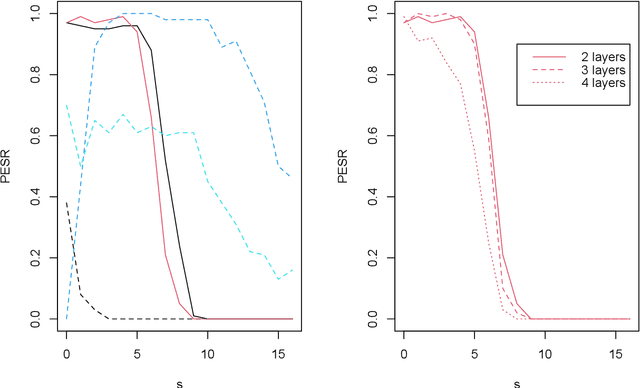
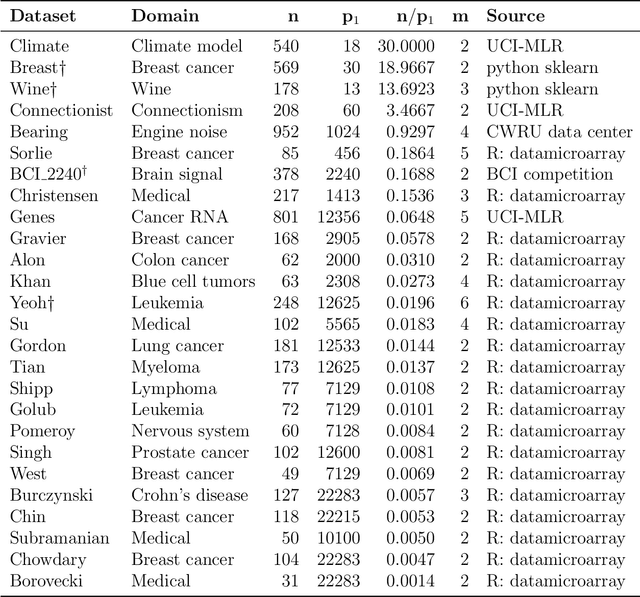
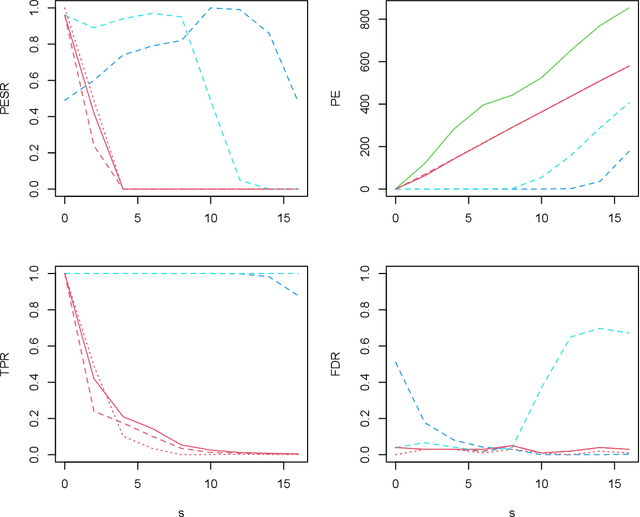
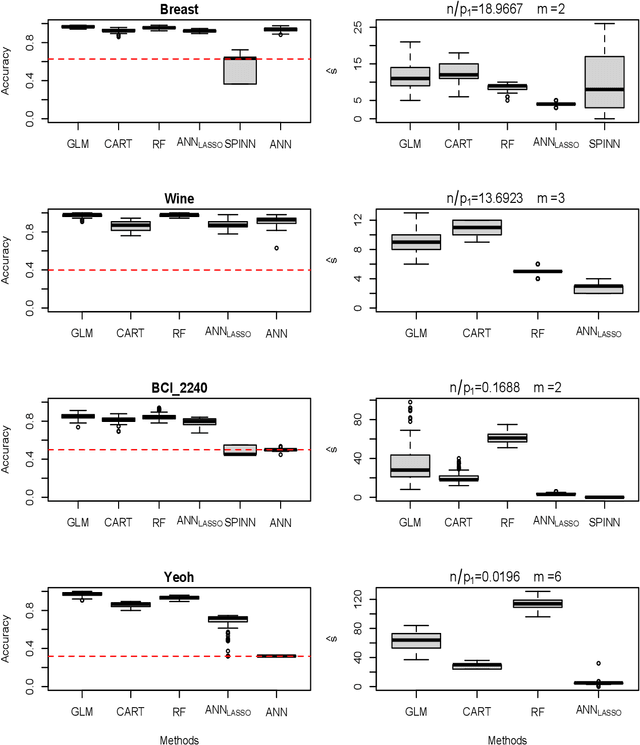
To fit sparse linear associations, a LASSO sparsity inducing penalty with a single hyperparameter provably allows to recover the important features (needles) with high probability in certain regimes even if the sample size is smaller than the dimension of the input vector (haystack). More recently learners known as artificial neural networks (ANN) have shown great successes in many machine learning tasks, in particular fitting nonlinear associations. Small learning rate, stochastic gradient descent algorithm and large training set help to cope with the explosion in the number of parameters present in deep neural networks. Yet few ANN learners have been developed and studied to find needles in nonlinear haystacks. Driven by a single hyperparameter, our ANN learner, like for sparse linear associations, exhibits a phase transition in the probability of retrieving the needles, which we do not observe with other ANN learners. To select our penalty parameter, we generalize the universal threshold of Donoho and Johnstone (1994) which is a better rule than the conservative (too many false detections) and expensive cross-validation. In the spirit of simulated annealing, we propose a warm-start sparsity inducing algorithm to solve the high-dimensional, non-convex and non-differentiable optimization problem. We perform precise Monte Carlo simulations to show the effectiveness of our approach.

What needles do sparse neural networks find in nonlinear haystacks

Using a sparsity inducing penalty in artificial neural networks (ANNs) avoids over-fitting, especially in situations where noise is high and the training set is small in comparison to the number of features. For linear models, such an approach provably also recovers the important features with high probability in regimes for a well-chosen penalty parameter. The typical way of setting the penalty parameter is by splitting the data set and performing the cross-validation, which is (1) computationally expensive and (2) not desirable when the data set is already small to be further split (for example, whole-genome sequence data). In this study, we establish the theoretical foundation to select the penalty parameter without cross-validation based on bounding with a high probability the infinite norm of the gradient of the loss function at zero under the zero-feature assumption. Our approach is a generalization of the universal threshold of Donoho and Johnstone (1994) to nonlinear ANN learning. We perform a set of comprehensive Monte Carlo simulations on a simple model, and the numerical results show the effectiveness of the proposed approach.