Robustness to Label Noise Depends on the Shape of the Noise Distribution in Feature Space

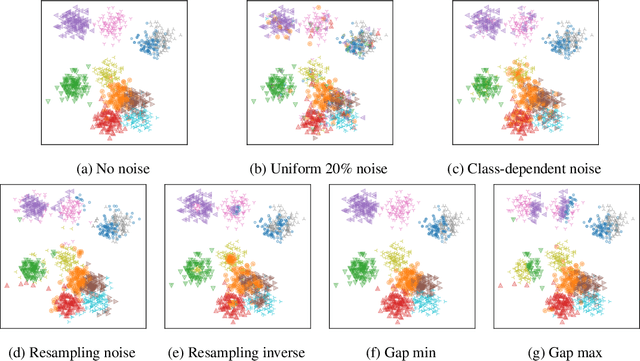
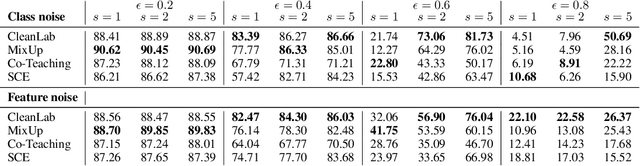
Machine learning classifiers have been demonstrated, both empirically and theoretically, to be robust to label noise under certain conditions -- notably the typical assumption is that label noise is independent of the features given the class label. We provide a theoretical framework that generalizes beyond this typical assumption by modeling label noise as a distribution over feature space. We show that both the scale and the shape of the noise distribution influence the posterior likelihood; and the shape of the noise distribution has a stronger impact on classification performance if the noise is concentrated in feature space where the decision boundary can be moved. For the special case of uniform label noise (independent of features and the class label), we show that the Bayes optimal classifier for $c$ classes is robust to label noise until the ratio of noisy samples goes above $\frac{c-1}{c}$ (e.g. 90% for 10 classes), which we call the tipping point. However, for the special case of class-dependent label noise (independent of features given the class label), the tipping point can be as low as 50%. Most importantly, we show that when the noise distribution targets decision boundaries (label noise is directly dependent on feature space), classification robustness can drop off even at a small scale of noise. Even when evaluating recent label-noise mitigation methods we see reduced accuracy when label noise is dependent on features. These findings explain why machine learning often handles label noise well if the noise distribution is uniform in feature-space; yet it also points to the difficulty of overcoming label noise when it is concentrated in a region of feature space where a decision boundary can move.

A phase transition for finding needles in nonlinear haystacks with LASSO artificial neural networks

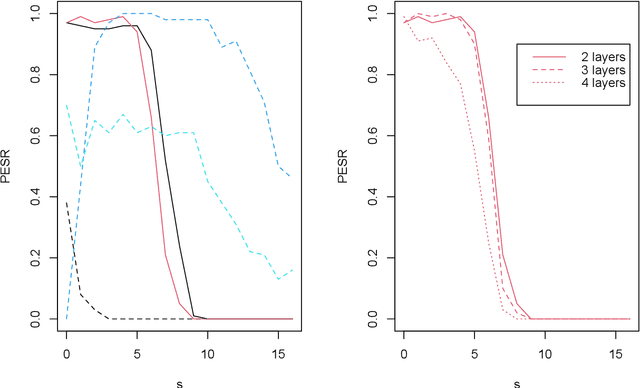
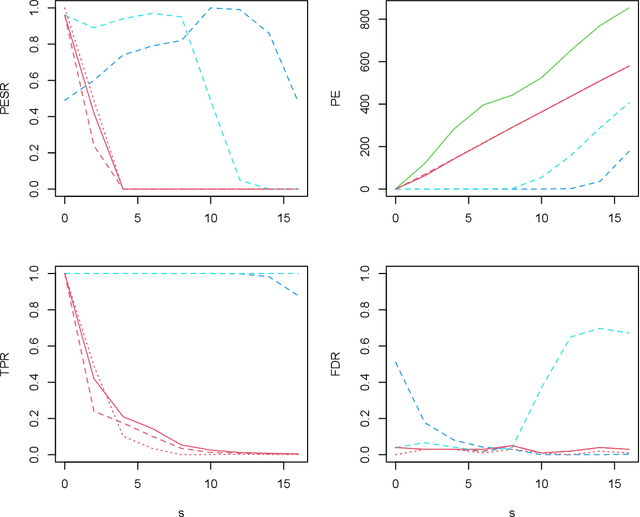
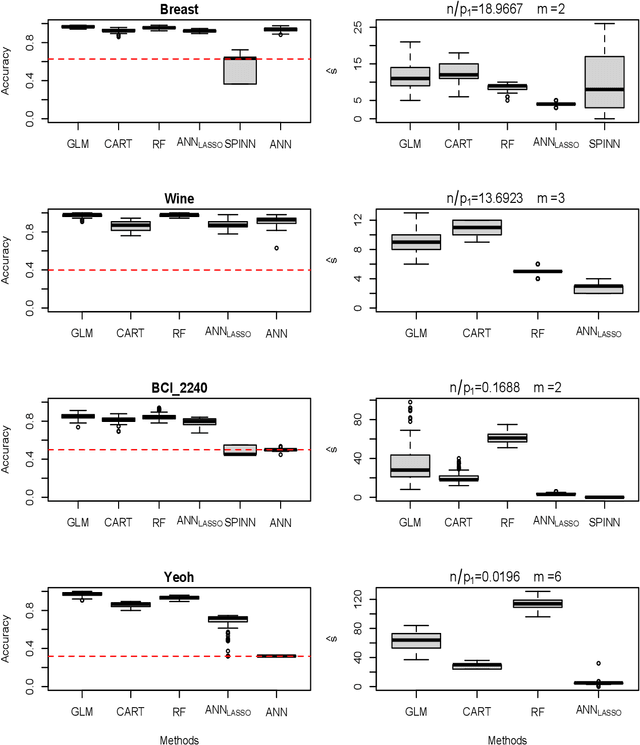
To fit sparse linear associations, a LASSO sparsity inducing penalty with a single hyperparameter provably allows to recover the important features (needles) with high probability in certain regimes even if the sample size is smaller than the dimension of the input vector (haystack). More recently learners known as artificial neural networks (ANN) have shown great successes in many machine learning tasks, in particular fitting nonlinear associations. Small learning rate, stochastic gradient descent algorithm and large training set help to cope with the explosion in the number of parameters present in deep neural networks. Yet few ANN learners have been developed and studied to find needles in nonlinear haystacks. Driven by a single hyperparameter, our ANN learner, like for sparse linear associations, exhibits a phase transition in the probability of retrieving the needles, which we do not observe with other ANN learners. To select our penalty parameter, we generalize the universal threshold of Donoho and Johnstone (1994) which is a better rule than the conservative (too many false detections) and expensive cross-validation. In the spirit of simulated annealing, we propose a warm-start sparsity inducing algorithm to solve the high-dimensional, non-convex and non-differentiable optimization problem. We perform precise Monte Carlo simulations to show the effectiveness of our approach.