Training a neural netwok for data reduction and better generalization

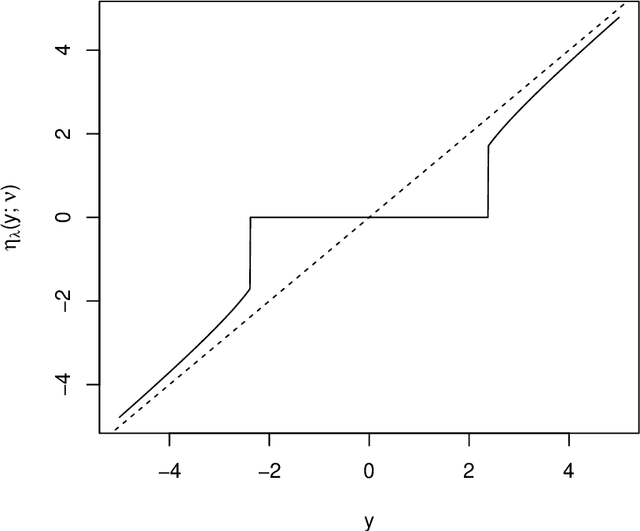
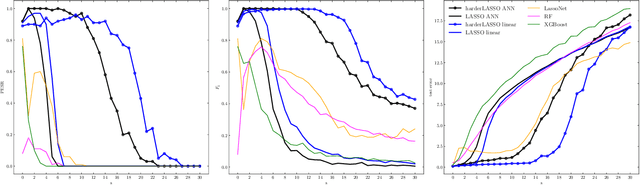
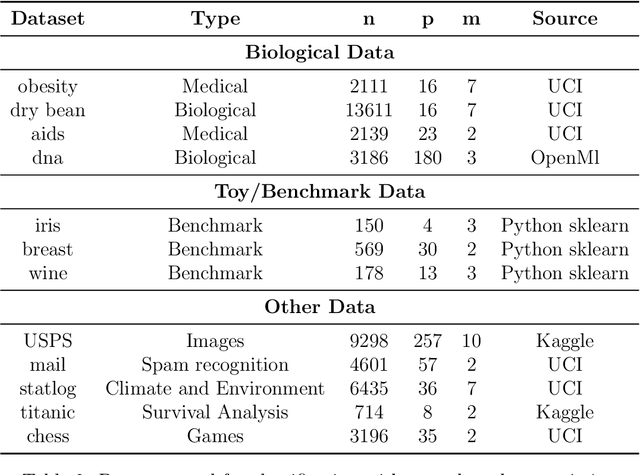
The motivation for sparse learners is to compress the inputs (features) by selecting only the ones needed for good generalization. Linear models with LASSO-type regularization achieve this by setting the weights of irrelevant features to zero, effectively identifying and ignoring them. In artificial neural networks, this selective focus can be achieved by pruning the input layer. Given a cost function enhanced with a sparsity-promoting penalty, our proposal selects a regularization term $\lambda$ (without the use of cross-validation or a validation set) that creates a local minimum in the cost function at the origin where no features are selected. This local minimum acts as a baseline, meaning that if there is no strong enough signal to justify a feature inclusion, the local minimum remains at zero with a high prescribed probability. The method is flexible, applying to complex models ranging from shallow to deep artificial neural networks and supporting various cost functions and sparsity-promoting penalties. We empirically show a remarkable phase transition in the probability of retrieving the relevant features, as well as good generalization thanks to the choice of $\lambda$, the non-convex penalty and the optimization scheme developed. This approach can be seen as a form of compressed sensing for complex models, allowing us to distill high-dimensional data into a compact, interpretable subset of meaningful features.

A phase transition for finding needles in nonlinear haystacks with LASSO artificial neural networks

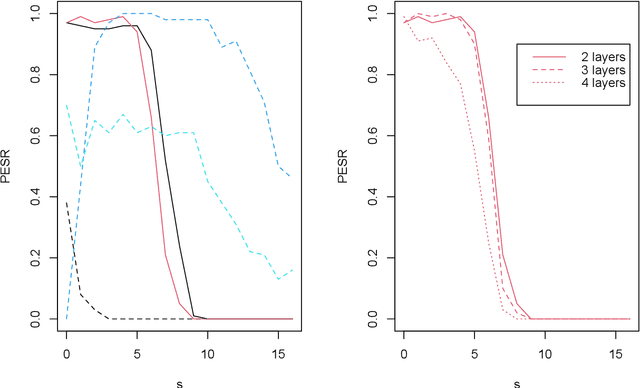
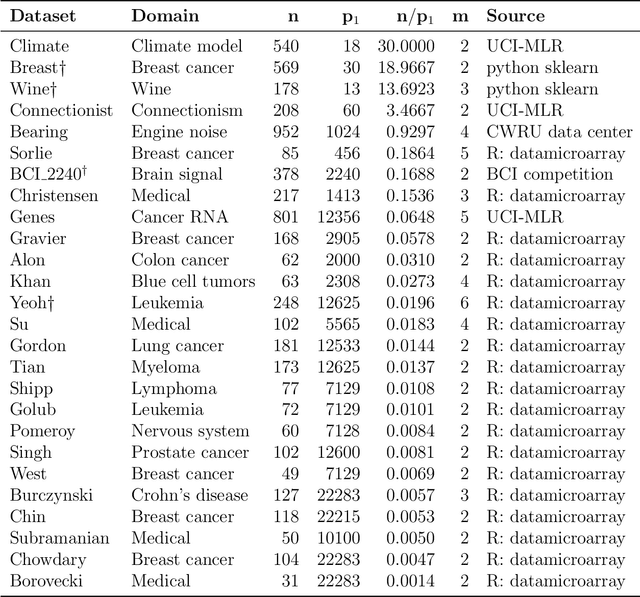
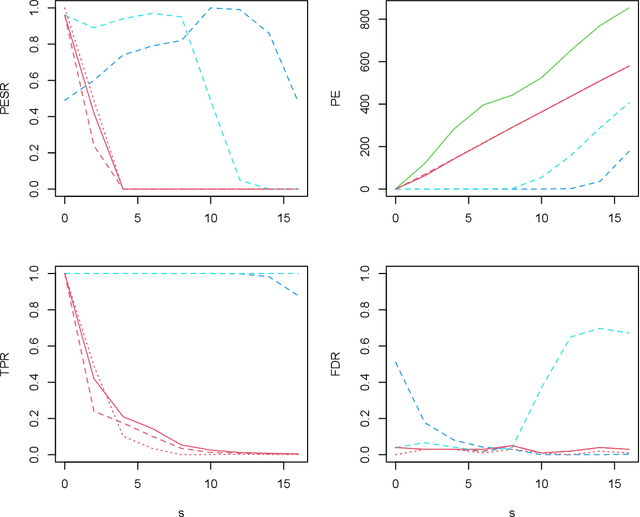
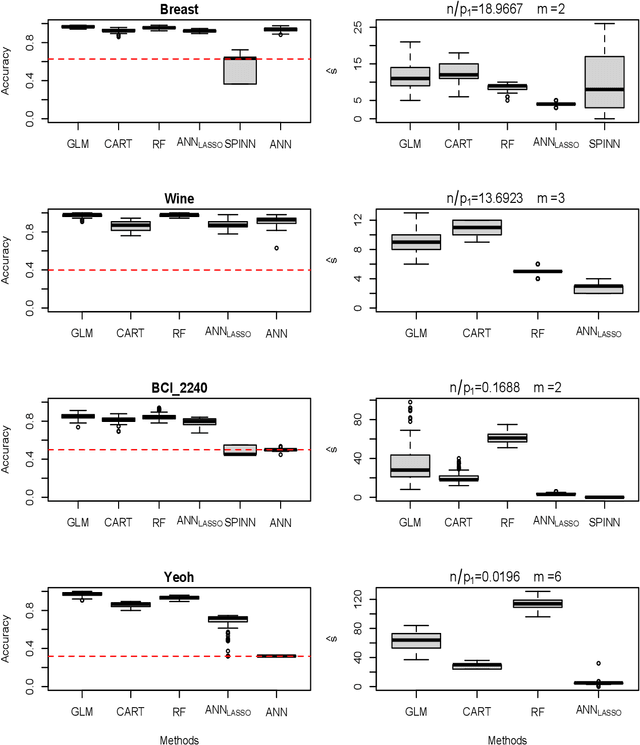
To fit sparse linear associations, a LASSO sparsity inducing penalty with a single hyperparameter provably allows to recover the important features (needles) with high probability in certain regimes even if the sample size is smaller than the dimension of the input vector (haystack). More recently learners known as artificial neural networks (ANN) have shown great successes in many machine learning tasks, in particular fitting nonlinear associations. Small learning rate, stochastic gradient descent algorithm and large training set help to cope with the explosion in the number of parameters present in deep neural networks. Yet few ANN learners have been developed and studied to find needles in nonlinear haystacks. Driven by a single hyperparameter, our ANN learner, like for sparse linear associations, exhibits a phase transition in the probability of retrieving the needles, which we do not observe with other ANN learners. To select our penalty parameter, we generalize the universal threshold of Donoho and Johnstone (1994) which is a better rule than the conservative (too many false detections) and expensive cross-validation. In the spirit of simulated annealing, we propose a warm-start sparsity inducing algorithm to solve the high-dimensional, non-convex and non-differentiable optimization problem. We perform precise Monte Carlo simulations to show the effectiveness of our approach.

What needles do sparse neural networks find in nonlinear haystacks

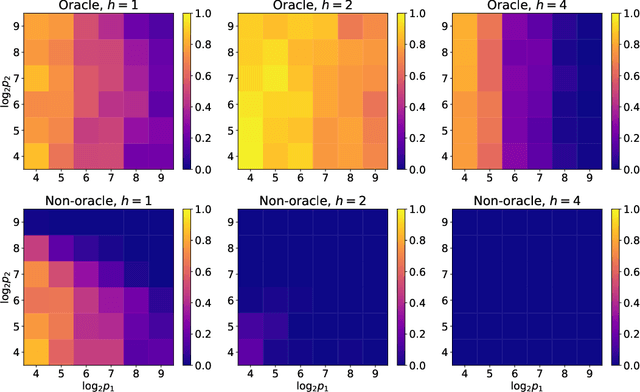
Using a sparsity inducing penalty in artificial neural networks (ANNs) avoids over-fitting, especially in situations where noise is high and the training set is small in comparison to the number of features. For linear models, such an approach provably also recovers the important features with high probability in regimes for a well-chosen penalty parameter. The typical way of setting the penalty parameter is by splitting the data set and performing the cross-validation, which is (1) computationally expensive and (2) not desirable when the data set is already small to be further split (for example, whole-genome sequence data). In this study, we establish the theoretical foundation to select the penalty parameter without cross-validation based on bounding with a high probability the infinite norm of the gradient of the loss function at zero under the zero-feature assumption. Our approach is a generalization of the universal threshold of Donoho and Johnstone (1994) to nonlinear ANN learning. We perform a set of comprehensive Monte Carlo simulations on a simple model, and the numerical results show the effectiveness of the proposed approach.

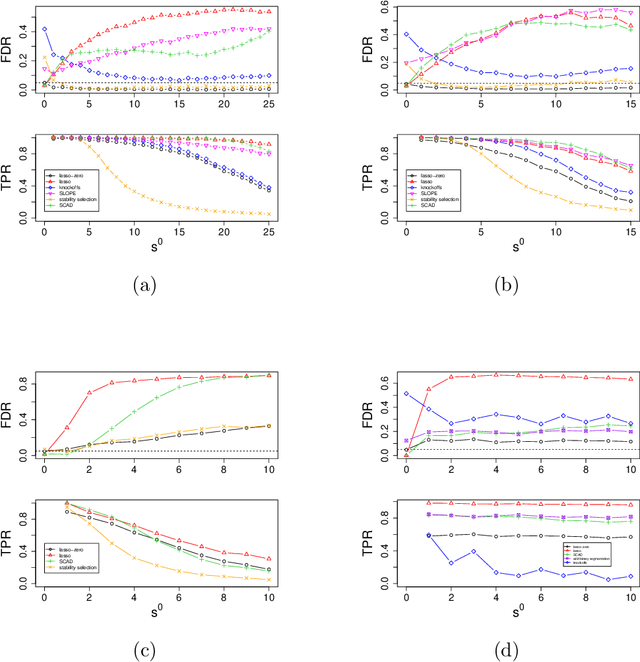
Robust Lasso-Zero for sparse corruption and model selection with missing covariates

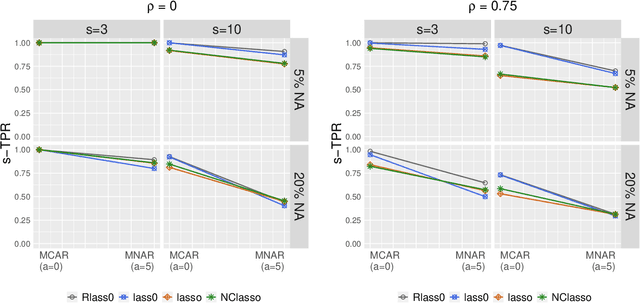
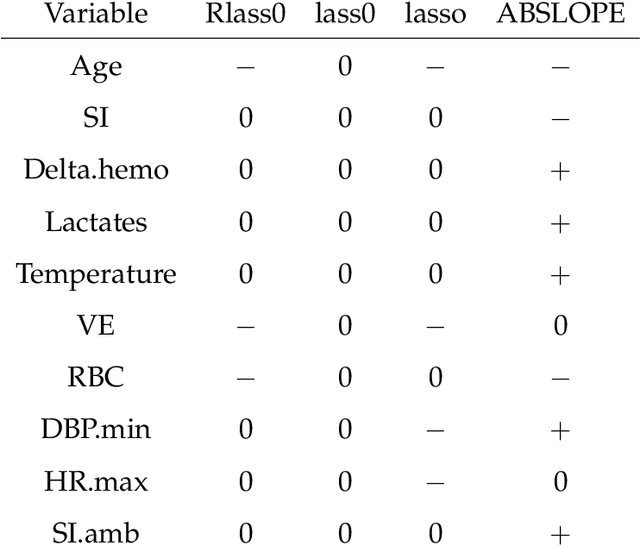
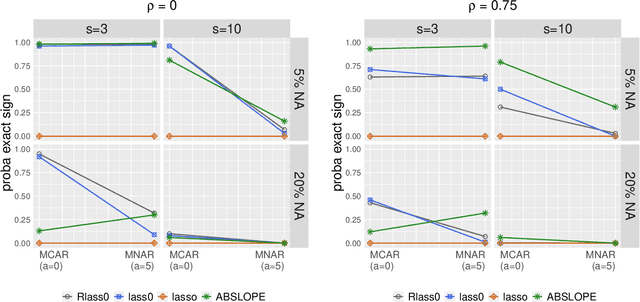
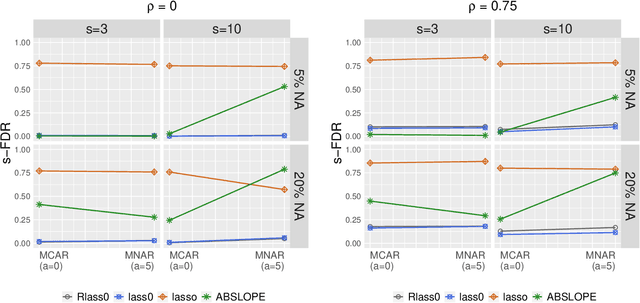
We propose Robust Lasso-Zero, an extension of the Lasso-Zero methodology [Descloux and Sardy, 2018], initially introduced for sparse linear models, to the sparse corruptions problem. We give theoretical guarantees on the sign recovery of the parameters for a slightly simplified version of the estimator, called Thresholded Justice Pursuit. The use of Robust Lasso-Zero is showcased for variable selection with missing values in the covariates. In addition to not requiring the specification of a model for the covariates, nor estimating their covariance matrix or the noise variance, the method has the great advantage of handling missing not-at random values without specifying a parametric model. Numerical experiments and a medical application underline the relevance of Robust Lasso-Zero in such a context with few available competitors. The method is easy to use and implemented in the R library lass0.

Model selection with lasso-zero: adding straw to the haystack to better find needles

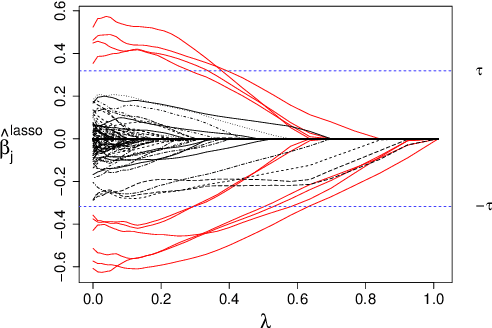
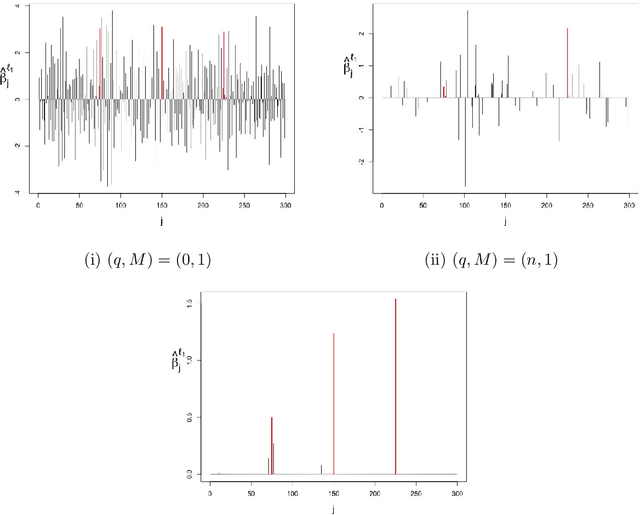
The high-dimensional linear model $y = X \beta^0 + \epsilon$ is considered and the focus is put on the problem of recovering the support $S^0$ of the sparse vector $\beta^0.$ We introduce lasso-zero, a new $\ell_1$-based estimator whose novelty resides in an "overfit, then threshold" paradigm and the use of noise dictionaries for overfitting the response. The methodology is supported by theoretical results obtained in the special case where no noise dictionary is used. In this case, lasso-zero boils down to thresholding the basis pursuit solution. We prove that this procedure requires weaker conditions on $X$ and $S^0$ than the lasso for exact support recovery, and controls the false discovery rate for orthonormal designs when tuned by the quantile universal threshold. However it requires a high signal-to-noise ratio, and the use of noise dictionaries addresses this issue. The threshold selection procedure is based on a pivotal statistic and does not require knowledge of the noise level. Numerical simulations show that lasso-zero performs well in terms of support recovery and provides a good trade-off between high true positive rate and low false discovery rate compared to competitors.

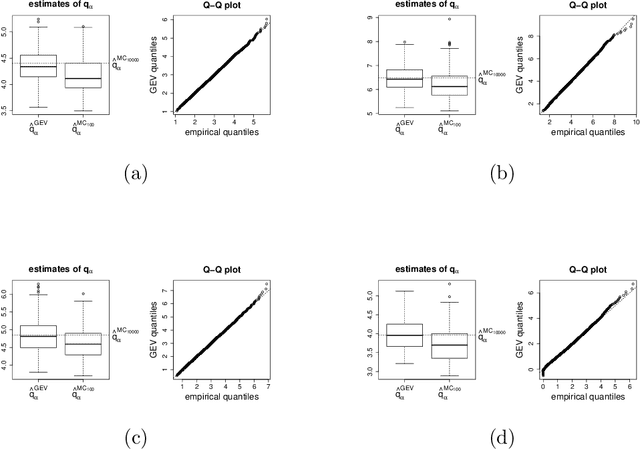
Quantile universal threshold: model selection at the detection edge for high-dimensional linear regression

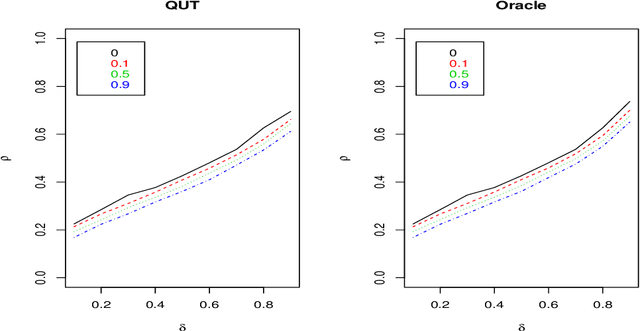
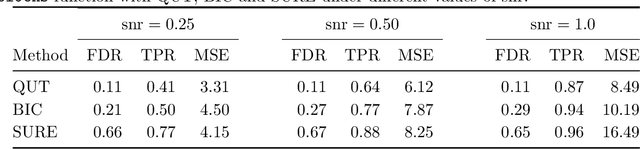
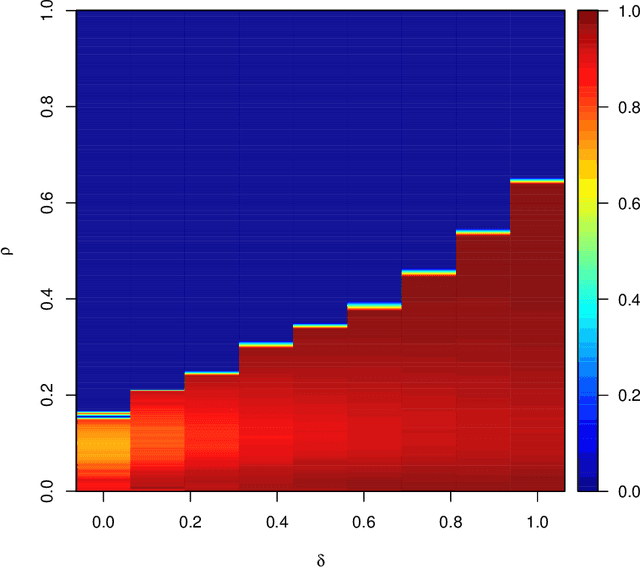
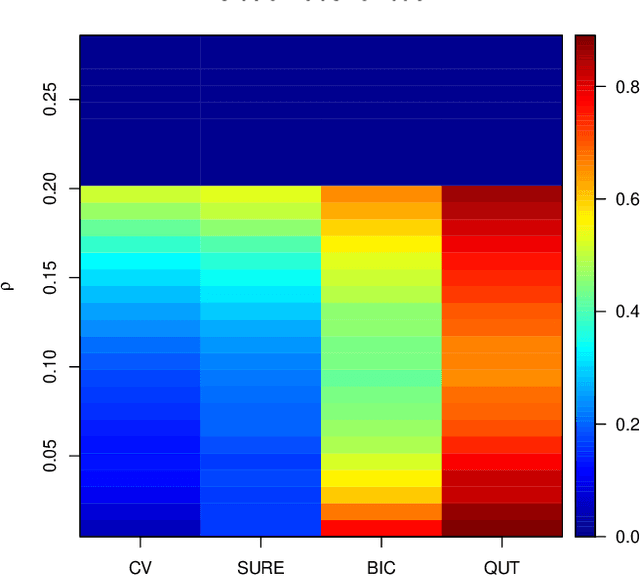
To estimate a sparse linear model from data with Gaussian noise, consilience from lasso and compressed sensing literatures is that thresholding estimators like lasso and the Dantzig selector have the ability in some situations to identify with high probability part of the significant covariates asymptotically, and are numerically tractable thanks to convexity. Yet, the selection of a threshold parameter $\lambda$ remains crucial in practice. To that aim we propose Quantile Universal Thresholding, a selection of $\lambda$ at the detection edge. We show with extensive simulations and real data that an excellent compromise between high true positive rate and low false discovery rate is achieved, leading also to good predictive risk.