Model selection with lasso-zero: adding straw to the haystack to better find needles

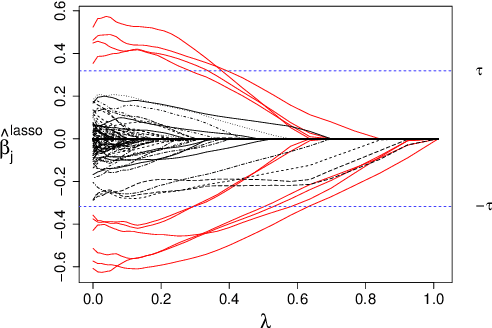
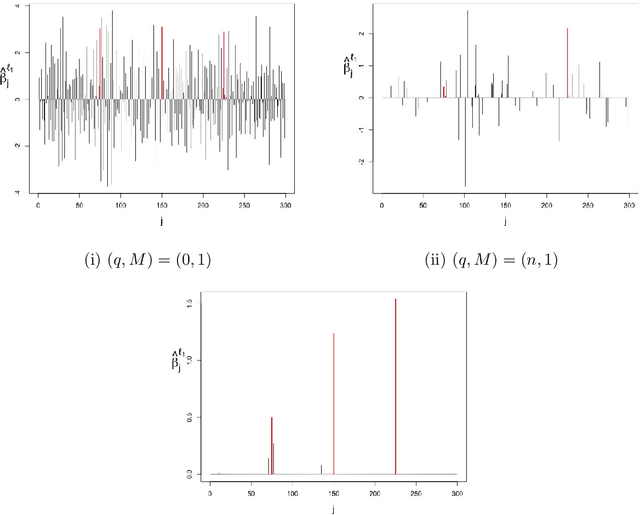
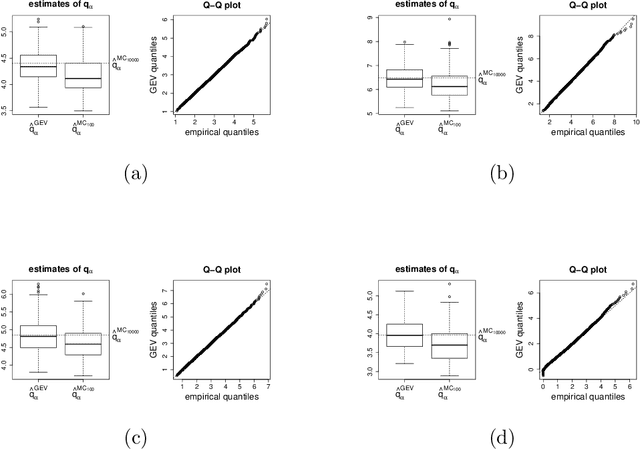
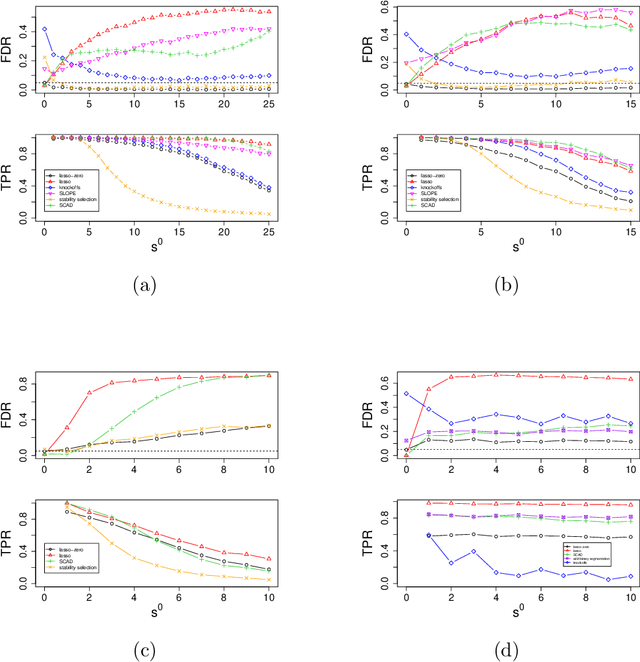
The high-dimensional linear model $y = X \beta^0 + \epsilon$ is considered and the focus is put on the problem of recovering the support $S^0$ of the sparse vector $\beta^0.$ We introduce lasso-zero, a new $\ell_1$-based estimator whose novelty resides in an "overfit, then threshold" paradigm and the use of noise dictionaries for overfitting the response. The methodology is supported by theoretical results obtained in the special case where no noise dictionary is used. In this case, lasso-zero boils down to thresholding the basis pursuit solution. We prove that this procedure requires weaker conditions on $X$ and $S^0$ than the lasso for exact support recovery, and controls the false discovery rate for orthonormal designs when tuned by the quantile universal threshold. However it requires a high signal-to-noise ratio, and the use of noise dictionaries addresses this issue. The threshold selection procedure is based on a pivotal statistic and does not require knowledge of the noise level. Numerical simulations show that lasso-zero performs well in terms of support recovery and provides a good trade-off between high true positive rate and low false discovery rate compared to competitors.