Fed-MIWAE: Federated Imputation of Incomplete Data via Deep Generative Models

Federated learning allows for the training of machine learning models on multiple decentralized local datasets without requiring explicit data exchange. However, data pre-processing, including strategies for handling missing data, remains a major bottleneck in real-world federated learning deployment, and is typically performed locally. This approach may be biased, since the subpopulations locally observed at each center may not be representative of the overall one. To address this issue, this paper first proposes a more consistent approach to data standardization through a federated model. Additionally, we propose Fed-MIWAE, a federated version of the state-of-the-art imputation method MIWAE, a deep latent variable model for missing data imputation based on variational autoencoders. MIWAE has the great advantage of being easily trainable with classical federated aggregators. Furthermore, it is able to deal with MAR (Missing At Random) data, a more challenging missing-data mechanism than MCAR (Missing Completely At Random), where the missingness of a variable can depend on the observed ones. We evaluate our method on multi-modal medical imaging data and clinical scores from a simulated federated scenario with the ADNI dataset. We compare Fed-MIWAE with respect to classical imputation methods, either performed locally or in a centralized fashion. Fed-MIWAE allows to achieve imputation accuracy comparable with the best centralized method, even when local data distributions are highly heterogeneous. In addition, thanks to the variational nature of Fed-MIWAE, our method is designed to perform multiple imputation, allowing for the quantification of the imputation uncertainty in the federated scenario.

Are labels informative in semi-supervised learning? -- Estimating and leveraging the missing-data mechanism

Semi-supervised learning is a powerful technique for leveraging unlabeled data to improve machine learning models, but it can be affected by the presence of ``informative'' labels, which occur when some classes are more likely to be labeled than others. In the missing data literature, such labels are called missing not at random. In this paper, we propose a novel approach to address this issue by estimating the missing-data mechanism and using inverse propensity weighting to debias any SSL algorithm, including those using data augmentation. We also propose a likelihood ratio test to assess whether or not labels are indeed informative. Finally, we demonstrate the performance of the proposed methods on different datasets, in particular on two medical datasets for which we design pseudo-realistic missing data scenarios.

Model-based Clustering with Missing Not At Random Data

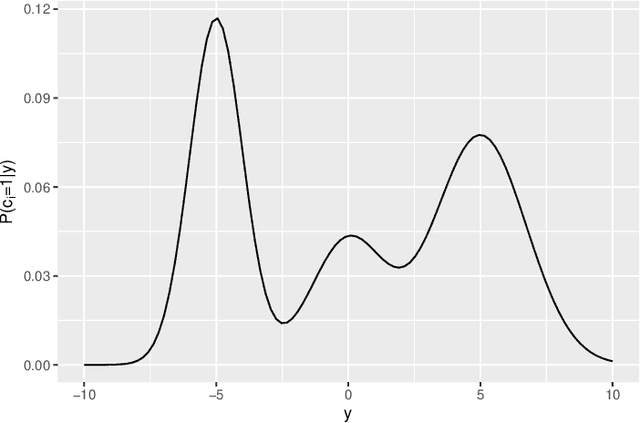
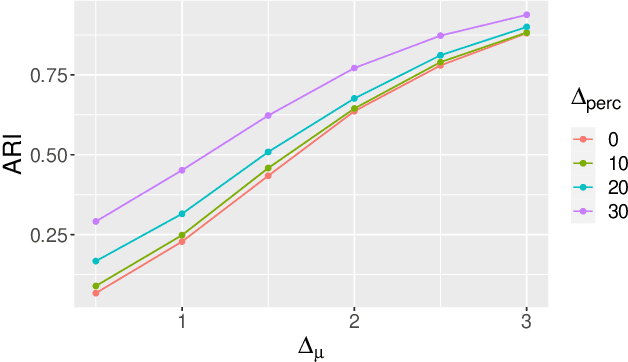
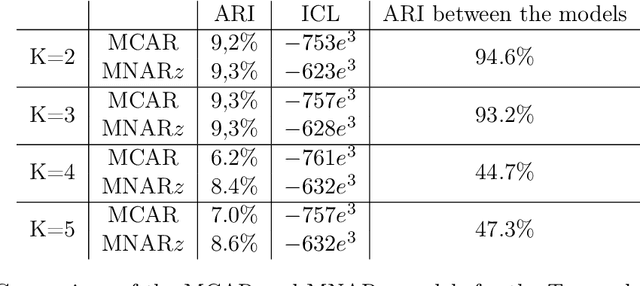
In recent decades, technological advances have made it possible to collect large data sets. In this context, the model-based clustering is a very popular, flexible and interpretable methodology for data exploration in a well-defined statistical framework. One of the ironies of the increase of large datasets is that missing values are more frequent. However, traditional ways (as discarding observations with missing values or imputation methods) are not designed for the clustering purpose. In addition, they rarely apply to the general case, though frequent in practice, of Missing Not At Random (MNAR) values, i.e. when the missingness depends on the unobserved data values and possibly on the observed data values. The goal of this paper is to propose a novel approach by embedding MNAR data directly within model-based clustering algorithms. We introduce a selection model for the joint distribution of data and missing-data indicator. It corresponds to a mixture model for the data distribution and a general MNAR model for the missing-data mechanism, which may depend on the underlying classes (unknown) and/or the values of the missing variables themselves. A large set of meaningful MNAR sub-models is derived and the identifiability of the parameters is studied for each of the sub-models, which is usually a key issue for any MNAR proposals. The EM and Stochastic EM algorithms are considered for estimation. Finally, we perform empirical evaluations for the proposed submodels on synthetic data and we illustrate the relevance of our method on a medical register, the TraumaBase (R) dataset.

Robust Lasso-Zero for sparse corruption and model selection with missing covariates

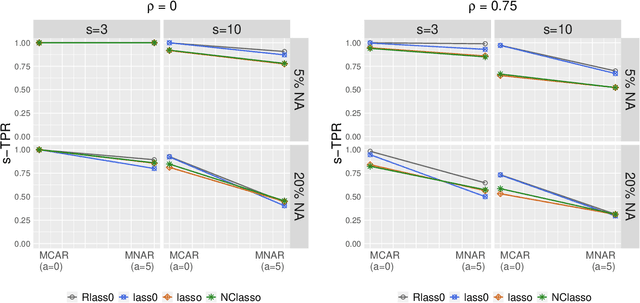
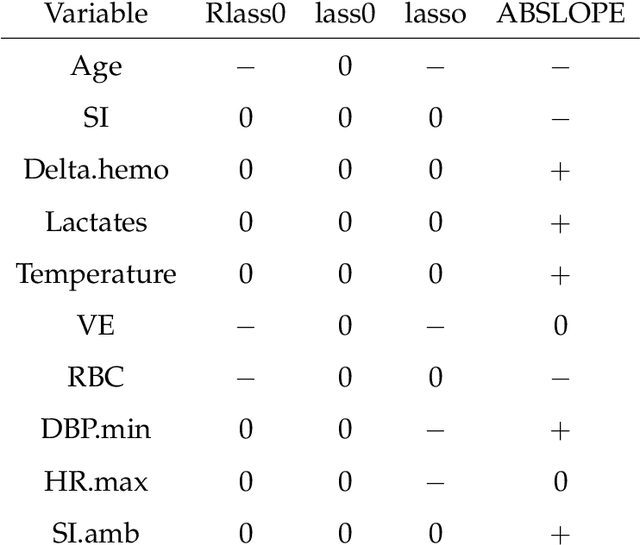
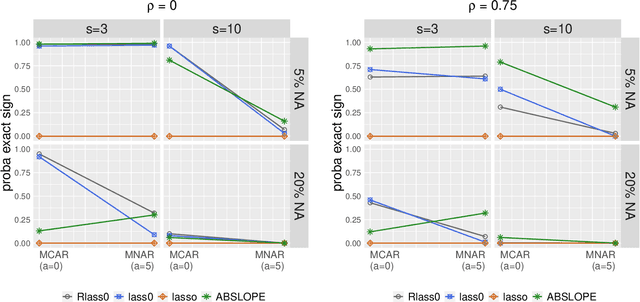
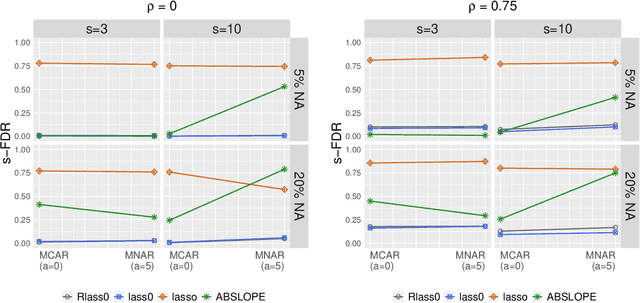
We propose Robust Lasso-Zero, an extension of the Lasso-Zero methodology [Descloux and Sardy, 2018], initially introduced for sparse linear models, to the sparse corruptions problem. We give theoretical guarantees on the sign recovery of the parameters for a slightly simplified version of the estimator, called Thresholded Justice Pursuit. The use of Robust Lasso-Zero is showcased for variable selection with missing values in the covariates. In addition to not requiring the specification of a model for the covariates, nor estimating their covariance matrix or the noise variance, the method has the great advantage of handling missing not-at random values without specifying a parametric model. Numerical experiments and a medical application underline the relevance of Robust Lasso-Zero in such a context with few available competitors. The method is easy to use and implemented in the R library lass0.

Imputation and low-rank estimation with Missing Non At Random data

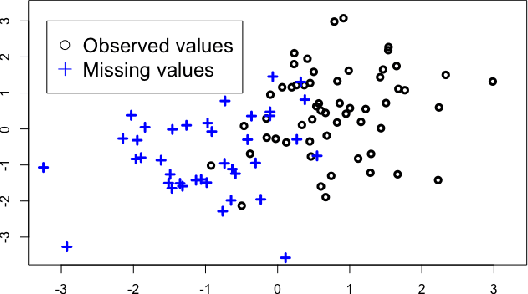
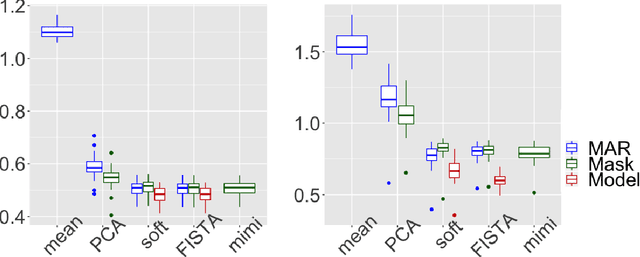
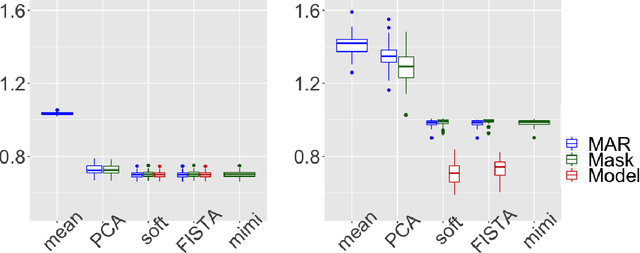
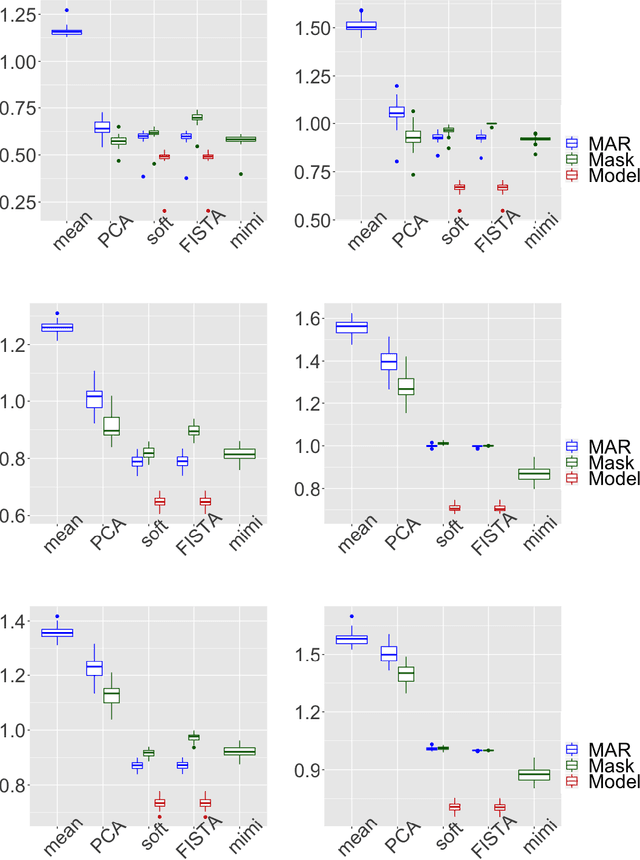
Missing values challenge data analysis because many supervised and unsu-pervised learning methods cannot be applied directly to incomplete data. Matrix completion based on low-rank assumptions are very powerful solution for dealing with missing values. However, existing methods do not consider the case of informative missing values which are widely encountered in practice. This paper proposes matrix completion methods to recover Missing Not At Random (MNAR) data. Our first contribution is to suggest a model-based estimation strategy by modelling the missing mechanism distribution. An EM algorithm is then implemented, involving a Fast Iterative Soft-Thresholding Algorithm (FISTA). Our second contribution is to suggest a computationally efficient surrogate estimation by implicitly taking into account the joint distribution of the data and the missing mechanism: the data matrix is concatenated with the mask coding for the missing values ; a low-rank structure for exponential family is assumed on this new matrix, in order to encode links between variables and missing mechanisms. The methodology that has the great advantage of handling different missing value mechanisms is robust to model specification errors.