Comparative study of clustering models for multivariate time series from connected medical devices

In healthcare, patient data is often collected as multivariate time series, providing a comprehensive view of a patient's health status over time. While this data can be sparse, connected devices may enhance its frequency. The goal is to create patient profiles from these time series. In the absence of labels, a predictive model can be used to predict future values while forming a latent cluster space, evaluated based on predictive performance. We compare two models on Withing's datasets, M AGMAC LUST which clusters entire time series and DGM${}^2$ which allows the group affiliation of an individual to change over time (dynamic clustering).

An iterative clustering algorithm for the Contextual Stochastic Block Model with optimality guarantees

Real-world networks often come with side information that can help to improve the performance of network analysis tasks such as clustering. Despite a large number of empirical and theoretical studies conducted on network clustering methods during the past decade, the added value of side information and the methods used to incorporate it optimally in clustering algorithms are relatively less understood. We propose a new iterative algorithm to cluster networks with side information for nodes (in the form of covariates) and show that our algorithm is optimal under the Contextual Symmetric Stochastic Block Model. Our algorithm can be applied to general Contextual Stochastic Block Models and avoids hyperparameter tuning in contrast to previously proposed methods. We confirm our theoretical results on synthetic data experiments where our algorithm significantly outperforms other methods, and show that it can also be applied to signed graphs. Finally we demonstrate the practical interest of our method on real data.

Model-based Clustering with Missing Not At Random Data

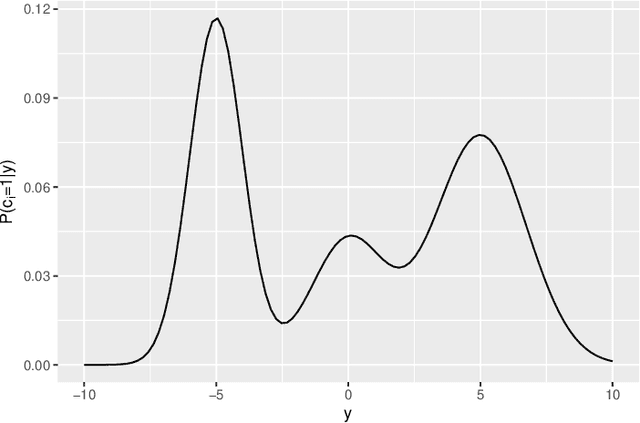
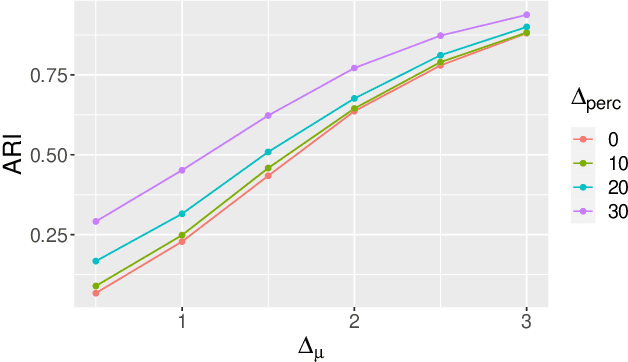
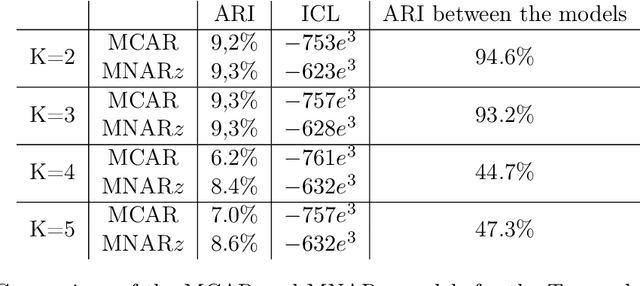
In recent decades, technological advances have made it possible to collect large data sets. In this context, the model-based clustering is a very popular, flexible and interpretable methodology for data exploration in a well-defined statistical framework. One of the ironies of the increase of large datasets is that missing values are more frequent. However, traditional ways (as discarding observations with missing values or imputation methods) are not designed for the clustering purpose. In addition, they rarely apply to the general case, though frequent in practice, of Missing Not At Random (MNAR) values, i.e. when the missingness depends on the unobserved data values and possibly on the observed data values. The goal of this paper is to propose a novel approach by embedding MNAR data directly within model-based clustering algorithms. We introduce a selection model for the joint distribution of data and missing-data indicator. It corresponds to a mixture model for the data distribution and a general MNAR model for the missing-data mechanism, which may depend on the underlying classes (unknown) and/or the values of the missing variables themselves. A large set of meaningful MNAR sub-models is derived and the identifiability of the parameters is studied for each of the sub-models, which is usually a key issue for any MNAR proposals. The EM and Stochastic EM algorithms are considered for estimation. Finally, we perform empirical evaluations for the proposed submodels on synthetic data and we illustrate the relevance of our method on a medical register, the TraumaBase (R) dataset.

Clustering multilayer graphs with missing nodes

Relationship between agents can be conveniently represented by graphs. When these relationships have different modalities, they are better modelled by multilayer graphs where each layer is associated with one modality. Such graphs arise naturally in many contexts including biological and social networks. Clustering is a fundamental problem in network analysis where the goal is to regroup nodes with similar connectivity profiles. In the past decade, various clustering methods have been extended from the unilayer setting to multilayer graphs in order to incorporate the information provided by each layer. While most existing works assume - rather restrictively - that all layers share the same set of nodes, we propose a new framework that allows for layers to be defined on different sets of nodes. In particular, the nodes not recorded in a layer are treated as missing. Within this paradigm, we investigate several generalizations of well-known clustering methods in the complete setting to the incomplete one and prove some consistency results under the Multi-Layer Stochastic Block Model assumption. Our theoretical results are complemented by thorough numerical comparisons between our proposed algorithms on synthetic data, and also on real datasets, thus highlighting the promising behaviour of our methods in various settings.